练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    函数y=ax2(a≠0)的图象经过点(a，8)，则a的值为（）

    A. ±2 B. －2 C. 2 D. 3

    C 【解析】把点(a，8)代入：y=ax2得：a3=8，解得：a=2. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

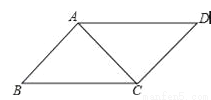
    如图，AC⊥AB，AC⊥CD，要使得△ABC≌△CDA．

    （1）若以“SAS”为依据，需添加条件____________；

    （2）若以“HL”为依据，需添加条件_____________．

    AB=CD AD=BC 【解析】(1)若以“SAS”为依据，需添加条件：AB=CD； ∵AC⊥AB，AC⊥CD， ∴∠BAC=90°，∠DCA=90°， ∴∠BAC=∠DCA， 在△ABC和△CDA中， ， ∴△ABC≌△CDA(SAS)； (2)若以“HL”为依据，需添加条件：AD=BC； 在Rt△ABC和Rt△CDA中， ∴Rt△ABC≌R...

    查看答案和解析>>

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：解答题

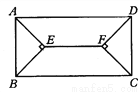
    如图所示，在矩形ABCD中，四个内角平分线相交于E、F， 若AB= 8cm，Ad=20cm，求EF的长度．

    12cm 【解析】试题分析：延长BE交AD于M，延长DF交BC于N，根据矩形的性质求出∠DAE=∠BAE=∠ABE=∠CBE=45°，AD∥BC，AD=BC，求出AE⊥BM，AB=AM，得出平行四边形BMDN和平行四边形EFDM，即可求出EF=DM，求出DM即可． 试题解析：延长BE交AD于M，延长DF交BC于N， ∵四边形ABCD是矩形， ∴∠DAB=∠ABC=∠BCD=...

    查看答案和解析>>

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：单选题

    E为矩形ABCD的边CD上的一点，AB=AE=4，BC=2，则∠BEC是（ ）．

    A. 15° B. 30° C. 60° D. 75°

    D 【解析】∵在Rt△ADE中，AD=2，AE=4， ∴∠AED=30°， ∵AB∥CD，∴∠EAB=∠AED=30°， ∵AB=AE， ∴∠AEB=75°， ∴∠BEC=180°-∠AED-∠AEB=180°-30°-75°=75°． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    平行四边形也是轴对称图形其对称轴也是对角线．（ ）

    × 【解析】平行四边形不是 但是特殊的平行四边形，如矩形、菱形、正方形等是轴对称图形，但一般的平行四边形不是轴对称图形， 所以原语句是错误的.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型：单选题

    若对任意实数x，二次函数y=(a+1)x2的值总是非负数，则a的取值范围是（）

    A. a≥－1 B. a≤－1 C. a>－1 D. a<－1

    C 【解析】∵若对任意实数x，二次函数y=(a+1)x2的值总是非负数， ∴其图象开口应该向上， ∴a+1>0，解得a>-1. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型：填空题

    写出一个开口向上，顶点是坐标原点的二次函数的解析式：___.

    y=2x2 【解析】图象的顶点在原点，开口向上的二次函数很多，如： .

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 25.1.1随机事件 测试 题型：解答题

    一个袋子中装有除颜色外都相同的6个红球和4个黄球,从袋子中任意摸出一个球,请问:

    (1)“摸出的球是白球”是什么事件?

    (2)“摸出的球是红球”是什么事件?

    (3)“摸出的球不是绿球”是什么事件?

    (4)摸出哪种颜色球的可能性最大?

    （1）不可能事件；（2）随机事件；（3）必然事件；(4)摸出红球的可能性最大. 【解析】试题分析： （1）因为袋子里没有白球，所以“摸出的球是白球”是不可能事件； （2）因为装有除颜色外都相同的6个红球和4个黄球，所以“摸出的球是红球”是随机事件；（3）因为袋子里没有绿球，所以“摸出的球不是绿球”是必然事件； （4）因为袋子里红球多，黄球少，所以摸出红色球的可能性最大。 试...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

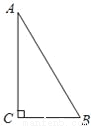
    如图所示，在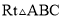中，∠C＝90°，∠A＝30°．

    （1）尺规作图：作线段AB的垂直平分线l（保留作图痕迹，不写作法）；

    （2）在已作的图形中，若l分别交AB、AC及BC的延长线于点D、E、F，连接BE，求证：EF＝2DE．

    （1）作图见解析；（2）证明见解析. 【解析】试题分析： （1）分别以点A，B为圆心，以大于AB的一半为半径画圆，两圆交于两点，过这两点画直线，这条直线即是线段AB的垂直平分线； （2）先证明ED=EC，再证∠F=30°，用含30°角的直角三角形的性质即可证明. 试题解析： 【解析】 （1）如下图所示，直线l即为所求． （2）证明：在Rt△ABC中，∵∠A＝3...

    查看答案和解析>>

    同步练习册答案