练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

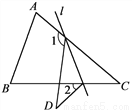
    如图，在△ABC中，∠C＝40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1－∠2的度数是（ ）

    A. 40° B. 80° C. 90° D. 140°

    B 【解析】 由题意得：∠C=∠D， ∵∠1=∠C+∠3，∠3=∠2+∠D， ∴∠1=∠2+∠C+∠D=∠2+2∠C， ∴∠1－∠2=2∠C=80°. 故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：解答题

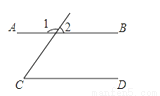
    已知：如图，∠1=120°，∠C=60°，判断AB与CD是否平行？为什么？

    见解析 【解析】试题分析： 根据平行线判定定理，要判断两直线是否平行，需找到是否有相关的同位角、内错角相等，或是同旁内角互补，由图可知只要判断出∠C与∠2这一对同位角是否相等即可. 【解析】 AB与CD是平行． 理由如下：∵∠1=120°， ∴∠2=180°﹣∠1=60°． 又∵∠C=60°， ∴∠2=∠C， ∴AB∥CD．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：单选题

    两道单选题都含A、B、C、D四个选项，瞎猜这两道题，恰好全部猜对的概率是（ ）

    A. B. C. D.

    D 【解析】试题解析：对于每一道题本身而言．猜对的概率为 设表示第一道选择题答对， 表示第二道选择题答对． 因为两道单项题之间没有联系．所以与相互独立． 故 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：填空题

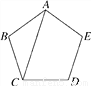
    如图，AC是正五边形ABCDE的一条对角线，则∠ACB＝_________.

    36° 【解析】试题解析：∵五边形ABCDE是正五边形， ∴∠B=108°，AB=CB， ∴∠ACB=（180°-108°）÷2=36°； 故答案为：36°．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：单选题

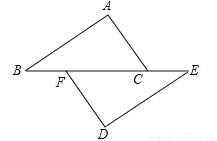
    如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（ ）

    A. AB=DE B. AC=DF C. ∠A=∠D D. BF=EC

    C 【解析】试题分析：【解析】 选项A、添加AB=DE可用AAS进行判定，故本选项错误； 选项B、添加AC=DF可用AAS进行判定，故本选项错误； 选项C、添加∠A=∠D不能判定△ABC≌△DEF，故本选项正确； 选项D、添加BF=EC可得出BC=EF，然后可用ASA进行判定，故本选项错误． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：解答题

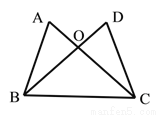
    （8分）已知：如图，AC与BD相交于点O，∠ABC=∠DCB，AB=DC，

    求证：∠OBC=∠OCB。

    见解析 【解析】试题分析：本题考查了全等三角形的判定与性质，根据SAS可判定△ABC≌△DCB，然后根据全等三角形的额对应角相等可证∠OBC=∠OCB. 证明：在△ABC和△DCB中 ∴△ABC≌△DCB ∴OBC=∠OCB

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：填空题

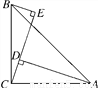
    如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D，AD＝2cm，BE＝0.5cm，则DE＝________cm.

    1.5 【解析】∵BE⊥CE于E，AD⊥CE于D ∴∠E=∠ADC=90° ∵∠BCE+∠ACE=∠DAC+∠ACE=90° ∴∠BCE=∠DAC ∵AC=BC ∴△ACD≌△CBE ∴CE=AD,BE=CD=2-0.5=1.5(cm).

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

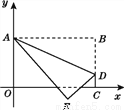
    如图，将长方形OABC置于平面直角坐标系中，点A的坐标为(0，4)，点C的坐标为(m，0)(m>0)，点D(m，1)在BC上，将长方形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E.

    （1）当m=3时，点B的坐标为_________，点E的坐标为_________; 

    （2）随着m的变化，试探索:点E能否恰好落在x轴上?若能，请求出m的值;若不能，请说明理由.

    （1）(3，4)，(0，1)；（2）点E能恰好落在x轴上，理由见解析. 【解析】试题分析：（1）根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标； （2）由折叠的性质求得线段DE和AE的长，然后利用勾股定理得到有关m的方程，求得m的值即可． 试题解析：（1）点B的坐标为（3，4）， ∵AB=BD=3， ∴△ABD是等腰直角三角形， ∴∠BAD=45...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，下列条件中不能判定△ACD∽△ABC的是（ ）

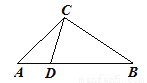
    A. 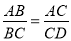B. ∠ADC＝∠ACB

    C. ∠ACD＝∠B D. AC2=AD·AB

    A 【解析】根据两边对应成比例且夹角相等，可由，∠B=∠B，可得△ACD∽△ABC，故A不能判定两三角形相似； 根据两角对应相等的两三角形相似，可知B、C均可以判定两三角形相似；根据两边对应成比例且夹角相等，可由AC2=AD·AB，∠A为公共角，可判定两三角形相似. 故选：A.

    查看答案和解析>>

    同步练习册答案