
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90º.解答下列问题:
(1) 如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为,数量关系为.(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?



(2) 如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?画出相应的图形,并说明理由.
见解析 【解析】试题分析:(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立; (2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图... 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证:△CAB≌△DEF.
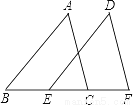
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,AB∥DE,CD=BF,若要证明△ABC≌△EDF,还需补充的条件是( )
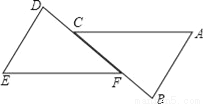
A. AC=EF B. AB=ED C. ∠B=∠E D. 不用补充
B 【解析】试题分析:根据平行线的性质得出∠B=∠D,求出BC=DF,根据全等三角形的判定定理逐个判断即可. 【解析】 AB=DE, 理由是:∵AB∥DE, ∴∠B=∠D, ∵BF=DC, ∴BC=DF, 在△ABC和△DEF中 , ∴△ABC≌△DEF(SAS),即选项B正确, 选项A、C、D都不能推出△ABC≌△DEF,即选项A、C...查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
已知关于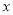 的分式方程
的分式方程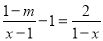 的解是正数,则
的解是正数,则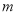 的取值范围是( )
的取值范围是( )
A. 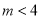 且
且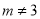 B.
B. 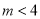
C. 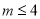 且
且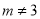 D.
D. 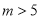 且
且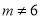
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
如果分式 的值为0,则
的值为0,则 的值为( )
的值为( )
A. -1 B. 1 C. ±1 D. 0
A 【解析】分式的值为0,分子为0分母不为0,由此可得 且x-1≠0,解得x=-1,故选A.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
如图,∠MON及ON上一点A.
求作:点P,使得PA⊥ON,且点P到∠MON两边的距离相等.
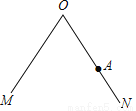
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:填空题
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.若PE=3,则点P到AB的距离是 .

查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
下列各式从左到右的变形中,是因式分解的为( )
A. 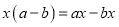 B.
B. 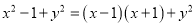
C. 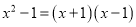 D.
D. 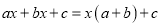
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
已知⊙O的直径为10 cm,圆心O到直线l的距离是 7 cm.,那么直线l和⊙O的位置关系是: ________.
相离 【解析】根据题意求出⊙O的半径为5,由和圆心O到直线l的距离是7cm,可知r<d,比较即可知直线l和⊙O的位置关系是相离. 故答案为:相离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com