练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

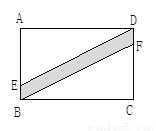
    如图，在矩形ABCD中，点E、F分别在AB、DC上，BF∥DE，若AD=12cm，AB=7cm，且AE：EB=5：2，则阴影部分的面积为_______

    24cm2． 【解析】试题分析：因为AD=12cm，AB=7cm，且AE：BE=5：2，则AE=5，BE=2， 则阴影部分的面积=12×7﹣12×5=24cm2． 故答案是24cm2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：填空题

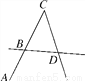
    如图，图中的线段共有________条，直线共有________条．

    3 1 【解析】试题分析：根据线段和直线的性质可知：本图中的线段有：线段BC，线段CD和线段BD，共3条；直线有：直线BD，共1条．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：解答题

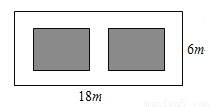
    如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60米2，两块绿地之间及周边留有宽度相等的人行通道．求人行通道的宽度．

    人行通道的宽度为1米 【解析】试题分析：设人行道的宽度为x米，根据矩形绿地的面积之和为60米2，列出一元二次方程． 设人行道的宽度为x米(0

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：单选题

    下列说法正确的是 （ ）

    A. “经过有交通信号的路口遇到红灯”是必然事件

    B. 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次

    C. 投掷一枚硬币正面朝上是随机事件

    D. 明天太阳从东方升起是随机事件

    C 【解析】试题解析：A. “经过有交通信号的路口遇到红灯”是随机事件, 说法错误. B. 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次,说法错误. C. 投掷一枚硬币正面朝上是随机事件,说法正确. D. 明天太阳从东方升起是必然事件.说法错误. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：解答题

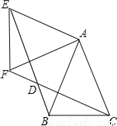
    如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D。

    （1）求证：BE＝CF ；

    （2）当四边形ACDE为菱形时，求BD的长。

    （1）证明见解析（2）-1 【解析】试题分析：（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD； （2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    如图，菱形ABCD中，AB=5，∠BCD=120°，则对角线AC的长是(　　)

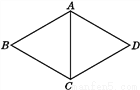
    A. 20 B. 15 C. 10 D. 5

    B 【解析】试题解析： 是菱形, 是等边三角形. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    正方形具有而菱形不具有的性质是

    A．四条边相等 B．对角线互相垂直平分

    C．对角线平分一组对角 D．对角线相等

    D 【解析】 试题分析：正方形的性质四条边相等，四个角相等对角线相等且垂直,互相平分．菱形的性质四条边相等，对角线垂直且互相平分．所以选D．

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：单选题

    （2011?德州）已知函数y=（x﹣a）（x﹣b）（其中a＞b）的图象如下面右图所示，则函数y=ax+b的图象可能正确的是（　　）

    A. B.

    C. D.

    D 【解析】分析：根据图象可得出方程（x-a）（x-b）=0的两个实数根为a，b，且一正一负，负数的绝对值大，又a＞b，则a＞0，b＜0．根据一次函数y=ax+b的图象的性质即可得出答案． 解答：【解析】 根据图象可得a，b异号， ∵a＞b，∴a＞0，b＜0， ∴函数y=ax+b的图象经过第一、三、四象限， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：填空题

    用等腰直角三角板画∠AOB=45°，将三角板沿OB方向平移到如图所示的虚线M处后绕点M逆时针旋转22°，则三角板的斜边与射线OA的夹角α为_____度．

    22 【解析】试题分析：如图： 由平移的性质知，AO∥SM， 故∠WMS=∠OWM=22°

    查看答案和解析>>

    同步练习册答案