
已知a、b是正实数,那么,![]() ≥
≥![]() 是恒成立的.
是恒成立的.
(1)由(![]() -
-![]() )2≥0恒成立,说明
)2≥0恒成立,说明![]() ≥
≥![]() 恒成立;
恒成立;
(2)填空:已知a、b、c是正实数,由![]() ≥
≥![]() 恒成立,猜测:
恒成立,猜测:![]() _
_![]() _也恒成立;
_也恒成立;
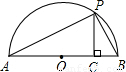
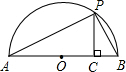
(3)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明![]() 恒成立.
恒成立.

|
分析.(1)由( (2)由a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ac)= (3)首先证得Rt△APC∽Rt△PBC,由相似三角形的对应边成比例,可求得PC的值,又由OP是半径,可求得OP= 解答.解:(1)∵( ∴a-2 ∴a+b≥2 ∴ (2) 理由:a3+b3+c3-3abc =(a+b+c)(a2+b2+c2-ab-bc-ac) = = ∵a、b、c是正实数, ∴a3+b3+c3-3abc≥0, ∴a3+b3+c3≥3abc, 同理: 故答案为: (3)如图,连接OP, ∵AB是直径, ∴∠APB=90°, 又∵PC⊥AB, ∴∠ACP=∠ACB=90°, ∴∠A+∠B=∠A+∠APC=90°, ∴∠APC=∠B, ∴Rt△APC∽Rt△PBC, ∴ ∴PC2=AC·CB=ab, ∴PC= 又∵PO= ∵PO≥PC, ∴
点评.此题考查了相似三角形的判定与性质、圆周角定理、几何不等式的应用与证明以及完全平方公式等知识.此题综合性较强,难度较大,注意数形结合思想的应用,注意完全平方式的非负性的应用. |
|
考点.相似三角形的判定与性质;完全平方公式;一元一次不等式的应用;圆周角定理. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么,| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b+c |
| 3 |
| 3 | abc |
| 3 | abc |
| a+b |
| 2 |
| ab |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知a,b是正实数,
已知a,b是正实数,| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川资阳卷)数学(带解析) 题型:解答题
已知a、b是正实数,那么,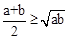 是恒成立的.
是恒成立的.
(1)(3分)由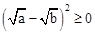 恒成立,说明
恒成立,说明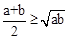 恒成立;
恒成立;
(2)(3分)填空:已知a、b、c是正实数,由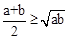 恒成立,猜测:
恒成立,猜测: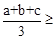 ▲ 也恒成立;
▲ 也恒成立;
(3)(2分)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明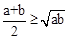 恒成立.
恒成立.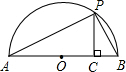
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
已知a、b是正实数,那么,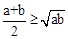 是恒成立的.
是恒成立的.
(1)(3分)由 恒成立,说明
恒成立,说明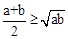 恒成立;
恒成立;
(2)(3分)填空:已知a、b、c是正实数,由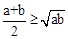 恒成立,猜测:
恒成立,猜测: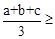 ▲ 也恒成立;
▲ 也恒成立;
(3)(2分)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明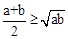 恒成立.
恒成立.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知a、b是正实数,那么,
已知a、b是正实数,那么, 是恒成立的.
是恒成立的.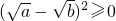 恒成立,说明
恒成立,说明 恒成立;
恒成立; 恒成立,猜测:
恒成立,猜测: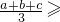 ______也恒成立;
______也恒成立; 恒成立.
恒成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com