解:(1)∵点E是两条内角平分线的交点,
∴∠EBC=

∠ABC,∠ECB=

∠ACB,
∴∠BEC=180°-

(∠ABC+∠ACB)=180°-

(180°-∠A)=90°+

∠A=120°,
∴∠A
1EC=180°-120°=60°;
(2)∵点F是两条外角平分线,
∴∠FBC=

(180°-∠ABC),∠ECB=

(180°-∠ACB),
∴∠BFC=180°-

(180°-∠ABC+180°-∠ACB)=

(∠ABC+∠ACB)=

(180°-∠A)=90°-

∠A=60°,
(3)∠A
1=

∠A.理由如下:
∵点A
1是内角∠ABC、外角∠ACD平分线的交点的交点.
∴∠ACD=2∠A
1CD,∠ABC=2∠A
1BD,
∵∠A
1=∠A
1CD-∠A
1BD,∠A=∠ACD-∠ABD,
∴∠A=2∠A
1CD-2∠A
1BD=2(∠A
1CD-∠A
1BD)
∴∠A=2∠A
1,
即∠A
1=

∠A;
(4)∠A
n=
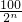
.
分析:(1)根据角平分线定义得到∠EBC=

∠ABC,∠ECB=

∠ACB,再根据三角形内角和定理得∠BEC=180°-

(∠ABC+∠ACB)=180°-

(180°-∠A),然后整理后把∠A=60°代入计算即可;
(2)根据角平分线定义得到∠FBC=

(180°-∠ABC),∠ECB=

(180°-∠ACB),再根据三角形内角和定理得∠BFC=180°-

(180°-∠ABC+180°-∠ACB)=

(∠ABC+∠ACB)=

(180°-∠A),然后把∠A=60°代入计算即可;
(3)根据角平分线定义得到∠ACD=2∠A
1CD,∠ABC=2∠A
1BD,再根据三角形外角性质得∠A
1=∠A
1CD-∠A
1BD,∠A=∠ACD-∠ABD,则∠A=2∠A
1CD-2∠A
1BD=2(∠A
1CD-∠A
1BD)=2∠A
1;
(4)根据(3)的结论可得到∠A
n=

,然后把∠A的度数代入即可.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形外角性质.

 如图,在△ABC中,∠A=60°,点E是两条内角平分线的交点,点F是两条外角平分线,点A1是内角∠ABC、外角∠ACD平分线的交点的交点.
如图,在△ABC中,∠A=60°,点E是两条内角平分线的交点,点F是两条外角平分线,点A1是内角∠ABC、外角∠ACD平分线的交点的交点. ∠ABC,∠ECB=
∠ABC,∠ECB= ∠ACB,
∠ACB, (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A=120°,
∠A=120°, (180°-∠ABC),∠ECB=
(180°-∠ABC),∠ECB= (180°-∠ACB),
(180°-∠ACB), (180°-∠ABC+180°-∠ACB)=
(180°-∠ABC+180°-∠ACB)= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)=90°-
(180°-∠A)=90°- ∠A=60°,
∠A=60°, ∠A.理由如下:
∠A.理由如下: ∠A;
∠A;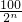 .
. ∠ABC,∠ECB=
∠ABC,∠ECB= ∠ACB,再根据三角形内角和定理得∠BEC=180°-
∠ACB,再根据三角形内角和定理得∠BEC=180°- (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A),然后整理后把∠A=60°代入计算即可;
(180°-∠A),然后整理后把∠A=60°代入计算即可; (180°-∠ABC),∠ECB=
(180°-∠ABC),∠ECB= (180°-∠ACB),再根据三角形内角和定理得∠BFC=180°-
(180°-∠ACB),再根据三角形内角和定理得∠BFC=180°- (180°-∠ABC+180°-∠ACB)=
(180°-∠ABC+180°-∠ACB)= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A),然后把∠A=60°代入计算即可;
(180°-∠A),然后把∠A=60°代入计算即可; ,然后把∠A的度数代入即可.
,然后把∠A的度数代入即可.

 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为