
 已知如图,矩形OABC的长OA=2
已知如图,矩形OABC的长OA=2 ,宽OC=2,将△AOC沿AC翻折得△AFC.
,宽OC=2,将△AOC沿AC翻折得△AFC. 解:(1)过F作FG⊥y轴于G.
解:(1)过F作FG⊥y轴于G. ,OC=2,
,OC=2,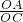 =
= ,
, CF=1,GF=
CF=1,GF= =
= ,
, ,-3);
,-3); ,0)、C(0,-2)、F(
,0)、C(0,-2)、F( ,-3),
,-3), ,
, ,
, ∴过A、F、C三点的抛物线解析式为y=
∴过A、F、C三点的抛物线解析式为y= x2-
x2- x-2; 8′
x-2; 8′ =
= ,
, AH.
AH. m2-
m2- m-2)(m<0),
m-2)(m<0), m2-
m2- m-2=
m-2= (-m+2
(-m+2 ),
), ,
, ,12),能够使得△ACP为以A为直角顶点的直角三角形.
,12),能够使得△ACP为以A为直角顶点的直角三角形.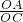 =
= ,则∠OCA=60°,再由轴对称的性质得出CF=OC=2,∠ACF=∠OCA=60°,则∠FCG=60°,然后解Rt△CFG,求出CG=1,GF=
,则∠OCA=60°,再由轴对称的性质得出CF=OC=2,∠ACF=∠OCA=60°,则∠FCG=60°,然后解Rt△CFG,求出CG=1,GF= ,进而得到点F的坐标;
,进而得到点F的坐标; =
= ,得出PH=
,得出PH= AH,设P(m,
AH,设P(m, m2-
m2- m-2)(m<0),得到关于m的方程,解方程求出m=-2
m-2)(m<0),得到关于m的方程,解方程求出m=-2 ,进而求出点P的坐标为(-2
,进而求出点P的坐标为(-2 ,12).
,12).

科目:初中数学 来源: 题型:
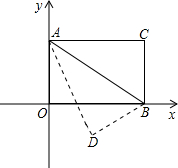 B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.查看答案和解析>>
科目:初中数学 来源:2010-2011学年辽宁省铁岭市昌图县太平中学九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《锐角三角函数》(03)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《图形的对称》(02)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《平面直角坐标系》(01)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com