
 .
. 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| b |
| a |
| a-b |
| a+b |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级上学期期末调研考试数学试卷(解析版) 题型:选择题
若α为锐角,且tanα= ,则有(??? )
,则有(??? )
A.0°<α<30°??? B.30°<α<45°
C.45°<α<60°?? D.60°<α<90°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,并适当加以文字说明.
,并适当加以文字说明. ,tanβ=
,tanβ= ,则α+β=45°.
,则α+β=45°. ,tanβ=
,tanβ=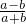 ,其中a>b>0,则α+β=45°.
,其中a>b>0,则α+β=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com