
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东临沂卷)数学解析版 题型:解答题
(2011•北京)阅读下面材料:
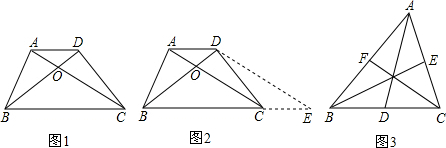
小伟遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).
参考小伟同学的思考问题的方法,解决下列问题:
如图3,△ABC的三条中线分别为AD,BE,CF.
(1)在图3中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹);
(2)若△ABC的面积为1,则以AD,BE,CF的长度为三边长的三角形的面积等于_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com