练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如下图：PC切⊙O于C，⊙O的割线PAB经过圆心O，并与⊙O交于A、B两点，PC＝8，PA＝4，求cosP的值

    答案：
    解析：

    　　连接OC，设⊙O的半径为R，在Rt△POC中，R2＋82＝(R＋4)2

    　　∴R＝6

    　　CosP＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：初中数学解题思路与方法 题型：044

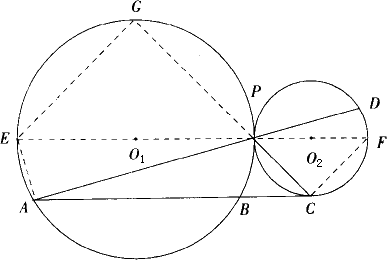
    已知如下图，⊙O1与⊙O2外切于点P，A为⊙O1上一点，直线AC切⊙O2于点C，交⊙O1于点B，AP的延长线交⊙O2于点D．若⊙O1半径是⊙O2半径的2倍，PD=10，AB＝7，求PC的长．

    查看答案和解析>>

    科目：初中数学 来源：宿迁市修远中学2007-2008学年度初三年级第一学期期中考试数学试卷(含答案) 题型：044

    如下图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC＝2.5．

    (1)当CE正好是⊙O的半径时，PT＝2，求⊙O的半径；

    (2)设PT2＝y，AC＝x，求出y与x之间的函数关系式；

    (3)△PTC能不能变为以PC为斜边的等腰直角三角形？若能，请求出△PTC的面积；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案