练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

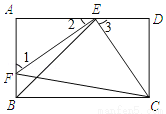
    如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．

    （1）求证：△AEF≌△DCE；

    （2）若CD=1，求BE的长．

    （1）证明见解析（2） 【解析】试题分析：（1）根据矩形的性质和已知条件可证明△AEF≌△DCE； （2）由（1）可知AE=DC，在Rt△ABE中由勾股定理可求得BE的长 试题解析：（1）证明：在矩形ABCD中，∠A=∠D=90°， ∴∠1+∠2=90°， ∵EF⊥EC， ∴∠FEC=90°， ∴∠2+∠3=90°， ∴∠1=∠3， 在△AEF...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：解答题

    对于平面直角坐标系中的任意两点P1(x1,y1)，P2(x2,y2)，我们把|x1－x2|+|y1－y2|叫做P1、P2两点间的直角距离，记作d(P1,P2)．

    (1) 令P0(2,－3)，O为坐标原点，则d(O,P0)＝ ；

    (2)已知O为坐标原点，动点P(x,y)满足d(O,P)＝1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；

    (3)设P0(x0,y0)是一定点，Q(x,y)是直线y=ax+b上的动点，我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离． 若P(a,－3)到直线y=x＋1的直角距离为6，求a的值．

    (1)5;(2)如图所示；（3）2或-10. 【解析】试题分析：（1）、根据直角距离的计算公式进行计算得出答案；（2）、根据题意得出|x|+|y|=1，从而得出图形；（3）、P（a，﹣3）到直线y=x+1的直角距离为6，设点Q的坐标为（x，x+1），从而得出|a﹣x|+|﹣3﹣x﹣1|=6，然后分情况得出a的值. 试题解析：（1）、根据题意得：d（O，P0）=|2﹣0|+|﹣3﹣0|=...

    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：单选题

    计算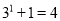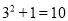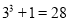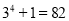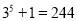： ， ， ， ， ， ，归纳各计算结果中的个位数字的规律，猜测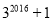的个位数字是（ ）

    A. 0 B. 2 C. 4 D. 8

    B 【解析】∵2016÷4=504, ∴即 +1的个位数字与的个位数字相同为2. 所以B选项是正确的.

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：解答题

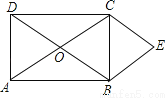
    平行四边形ABCD的对角线AC和BD交于O点，分别过顶点B，C作两对角线的平行线交于点E，得平行四边形OBEC．

    （1）如果四边形ABCD为矩形（如图），四边形OBEC为何种四边形？请证明你的结论；

    （2）当四边形ABCD是　 　 形时，四边形OBEC是正方形．

    （1）证明见解析；（2）正方 【解析】（1）根据矩形的性质：两条对角线相等且互相平分，即可得到结论；（2）根据正方形的性质：对角线相等且互相垂直平分，即可得到结论. 【解析】 （1）四边形OBEC是菱形．理由如下： ∵BE∥OC，CE∥OB， ∴四边形OBEC为平行四边形． 又∵四边形ABCD是矩形， ∴OC=AC; OB=BD；AC=BD ∴OC=OB...

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：单选题

    下列命题中，正确的是（　　）

    A. 四边相等的四边形是正方形

    B. 四角相等的四边形是正方形

    C. 对角线垂直的平行四边形是正方形

    D. 对角线相等的菱形是正方形

    D 【解析】试题分析：根据正方形的判定：对角线相等且互相垂直平分的四边形是正方形，对各个选项进行分析． 【解析】 A，错误，四边相等的四边形也可能是菱形； B，错误，矩形的四角相等，但不是正方形； C，错误，对角线垂直的平行四边形是菱形； D，正确，符合正方形的判定； 故选D．

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：填空题

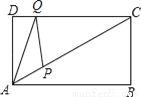
    如图，矩形ABCD中，AD=3，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是_____．

    3 【解析】作点A关于直线CD的对称点E，作EP⊥AC于P，交CD于点Q． ∵四边形ABCD是矩形， ∴∠ADC=90°， ∴DQ⊥AE，∵DE=AD， ∴QE=QA， ∴QA+QP=QE+QP=EP， ∴此时QA+QP最短（垂线段最短）， ∵∠CAB=30°， ∴∠DAC=60°， 在RT△APE中，∵∠APE=90°，AE=2AD=6...

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：单选题

    如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）

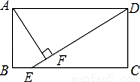
    A. △AFD≌△DCE B. AF=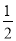AD C. AB=AF D. BE=AD﹣DF

    C 【解析】A．由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD∥BC，∴∠ADF=∠DEC． 又∵DE=AD，∴△AFD≌△DCE（AAS），故A正确； B．∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故B错误； C．由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故C正确； D．由△AF...

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：单选题

    如图中几何体的左视图是（）

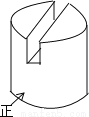
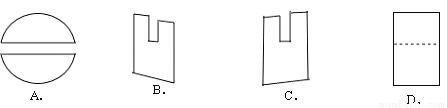
    A. A B. B C. C D. D

    D 【解析】【解析】 左视图是一个矩形，中间有条看不到的线，用虚线表示，故D正确．故选D．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省鸡西市虎林市八五八农场学校2018届九年级（上）期中考试数学试卷 题型：填空题

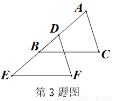
    如图，BC∥EF，AC∥DF，添加一个条件 ，使得△ABC≌△DEF．

    AB=DE或BC=EF或AC=DF 【解析】 试题解析：∵BC∥EF， ∴∠ABC=∠E， ∵AC∥DF， ∴∠A=∠EDF， ∵在△ABC和△DEF中， ， ∴△ABC≌△DEF， 同理，BC=EF或AC=DF也可求证△ABC≌△DEF．

    查看答案和解析>>

    同步练习册答案