

 ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ∠BAD,
∠BAD, (∠D+∠B),
(∠D+∠B), ×(40°+30°)=35°;
×(40°+30°)=35°; ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ∠BAD,
∠BAD,
 (∠D+∠B),
(∠D+∠B), ;
; ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ∠BAD,
∠BAD, ∠BCD=∠B+∠BAE-
∠BCD=∠B+∠BAE- (∠B+∠BAD+∠D)=
(∠B+∠BAD+∠D)= (∠B-∠D),
(∠B-∠D), .
. ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ∠BAD,则可得∠E=
∠BAD,则可得∠E= (∠D+∠B),继而求得答案;
(∠D+∠B),继而求得答案; ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ∠BAD,则可得∠E=
∠BAD,则可得∠E= (∠D+∠B),继而求得答案;
(∠D+∠B),继而求得答案;

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
 22、已知,如图,CA⊥BA于A,∠2+∠B=90°.
22、已知,如图,CA⊥BA于A,∠2+∠B=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,射线BA,BC相交成90°角,O是射线BC上一点,以点O为圆心,
如图,射线BA,BC相交成90°角,O是射线BC上一点,以点O为圆心,| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
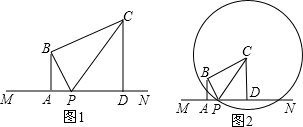
查看答案和解析>>
科目:初中数学 来源: 题型:
| DE |
| CF |
| AD |
| CD |
| DE |
| CF |
| AD |
| CD |
| DE |
| CF |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com