练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知∠AOB=36°，过点O画射线OC⊥OA、射线OD⊥OB 则∠COD=________°．

    36或144
    分析：首先根据题意画出图形，然后根据题意可求得各角的度数，注意图形的不同，答案不同．
    解答：解：∵OC⊥OA，OD⊥OB，
    ∴∠AOC=∠BOD=90°，
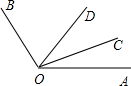
    如图（1），∵∠AOB=36°，∠AOB+∠AOD=∠AOD+∠COD=90°，
    ∴∠COD=∠AOB=36°；
    如图（2），∵∠AOB=36°，
    ∴∠BOC=90°-∠AOB=54°
    ∴∠COD=∠BOD+∠BOC=144°．
    ∴∠COD=36°或144°．
    故答案为：36或144．
    点评：此题考查了角的计算．此题难度不大，注意掌握分类讨论思想与数形结合思想的应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网几何计算题：
    （1）如图，已知∠BOC=4∠AOC，OD平分∠AOB，且∠COD=36°，求∠AOB的度数；
    （2）如图所示，已知AB：BC：CD=2：3：4，E、F分别为AB和CD的中点，且EF=12cm，求AD的长．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知在⊙O中，点A、B、C分别是圆上的三点，且∠AOB=72°，则∠ACB的度数为
    36°或144°
    36°或144°
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示为一弯形管道，其中心线是一段圆弧
    AB
    ．已知半径OA=60cm，∠AOB=108°，则管道的长度（即
    AB
    的长）为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知∠AOB=36°，过点O画射线OC⊥OA、射线OD⊥OB 则∠COD=
    36或144
    36或144
    °．

    查看答案和解析>>

    同步练习册答案