
 的平方根是_______;125的立方根是________.
的平方根是_______;125的立方根是________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果抛物线y=2x2与抛物线y=ax2关于x轴对称,那么a的值是_____.
-2 【解析】根据关于x轴对称的抛物线的开口方向改变,开口大小不变,可由抛物线y=2x2与抛物线y=ax2关于x轴对称,知两抛物线开口大小不变,方向相反,因此可得a=﹣2. 故答案为:﹣2.查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期九年级期末质量检测数学试卷 题型:解答题
如图,直线y=x+2与y轴交于点A,与反比例函数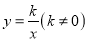 的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,求反比例函数的解析式.
的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,求反比例函数的解析式.
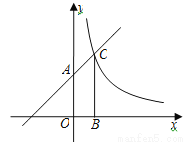
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期九年级期末质量检测数学试卷 题型:单选题
下列事件中,属于随机事件的有
①任意画一个三角形,其内角和为360°;
②投一枚骰子得到的点数是奇数;
③经过有交通信号灯的路口,遇到红灯;
④从日历本上任选一天为星期天.
A. ①②③ B. ②③④ C. ①③④ D. ①②④
B 【解析】试题解析:①是不可能事件, ②③④是随机事件. 故选B.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第六章达标检测卷 题型:解答题
求下列各数的平方根和算术平方根:(1)1; (2)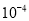 ;
;
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第六章达标检测卷 题型:单选题
在数轴上表示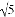 和-
和-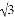 的两点间的距离是( )
的两点间的距离是( )
A. 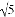 +
+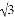 B.
B. 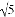 -
-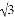 C. -(
C. -(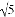 +
+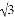 ) D.
) D. 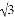 -
-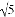
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:解答题
某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
【解析】 (1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意, 得:4x + 2(8-x)≥20,且x + 2(8-x)≥12, 解此不等式组,得 x≥2,且 x≤4,即 2≤x≤4 ∵ x是正整数,∴ x可取的值为2,3,4. 因此安排甲、乙两种货车有三种方案: 甲种货车 乙种货车 方案一 2辆 ...查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:单选题
某种出租车的收费标准:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米后,每增加1千米,加收2.4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费19元,那么甲地到乙地路程的最大值是( ).
A. 5千米 B. 7千米 C. 8千米 D. 15千米
C 【解析】试题分析:本题可先用19减去7得到12,则2.4(x﹣3)≤12,解出x的值,取最大整数即为本题的解. 【解析】 依题意得:2.4(x﹣3)≤19﹣7, 则2.4x﹣7.2≤12, 即2.4x≤19.2, ∴x≤8. 因此x的最大值为8. 故选:C.查看答案和解析>>
科目:初中数学 来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷 题型:解答题
(8分)如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数。
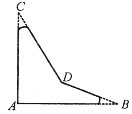
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com