练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知a＋1＝b＋2＝c＋3，求代数式(a－b)2＋(b－c)2＋(a－c)2的值．

    答案：6
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：学习周报　数学　沪科九年级版　2009－2010学年　第10期　总第166期 沪科版 题型：044

    “地震无情，人有情”，为了挽救受灾群众的生命，某地震救援队探测出某建筑物废墟下方的点C处有生命迹象．已知废墟一侧地面上的两个探测点A、B相距3米，探测线与地面的夹角分别为30°和60°(如图)，你能确定生命所在点C的深度吗？

    (提示：如图，过点C作CD⊥AB交AB的延长线于点D)．

    方法一：由题意知，∠ACB＝30°．所以△ABC为________三角形．所以BC＝AB＝3米．在Rt△BDC中，∠CBD＝60°，所以CD＝BC·________≈2.6(米)．

    所以生命所在点C的深度约为2.6米．

    方法二：因为探测线与地面的夹角分别为30°、60°，所以∠CAD＝30°，∠CBD＝60°．

    在Rt△BDC中，tan60°＝，所以BD＝________＝________．

    在Rt△ADC中，tan30°＝，所以AD＝________＝________．

    因为AB＝AD－BD＝3米，所以________－________＝3(米)．

    所以CD＝≈2.6(米)．

    所以生命所在点C的深度约为2.6米．

    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市2010年初中毕业生学业考试数学试题 题型：044

    如图1，已知∠ABC＝90°，△ABE是等边三角形，点P为射线BC上任意一点(点P与点B不重合)，连结AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连结QE并延长交射线BC于点F

    (1)如图2，当BP＝BA时，∠EBF＝________°，猜想∠QFC＝________°；

    (2)如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明；

    (3)已知线段AB＝，设BP＝x，点Q到射线BC的距离为y，求y关于x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将三角形纸片△ABC按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF。已知AB＝AC＝8，BC＝10，若以点B′，F，C为顶点的三角形与△ABC相似，那么BF的长度是______________.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    ．(10分)(1)如图1，已知点P在正三角形ABC的边BC上，以AP为边作正三角形APQ，连接CQ．
    ①求证：△ABP≌△ACQ；
    ②若AB＝6，点D是AQ的中点，直接写出当点P由点B运动到点C时，点D运动路线的长．
    (2)已知，△EFG中，EF＝EG＝13，FG＝10．如图2，把△EFG绕点E旋转到△EF＇G＇的位置，点M是边EF＇与边FG的交点，点N在边EG＇上且EN＝EM，连接GN．求点E到直线GN的距离．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏省南京市白下区中考二模数学试卷（解析版） 题型：解答题

    问题：已知线段AB、CD相交于点O，AB＝CD．连接AD、BC，请添加一个条件，使得△AOD≌△COB．

    小明的做法及思路

    小明添加了条件：∠DAB＝∠BCD．他的思路是：分两种情况画图①、图②，在两幅图中，

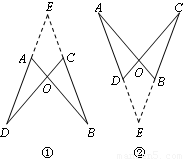
    都作直线DA、BC，两直线交于点E．

    由∠DAB＝∠BCD，可得∠EAB＝∠ECD．

    ∵AB＝CD，∠E＝∠E，

    ∴△EAB≌△ECD．∴EB＝ED，EA＝EC．

    图①中ED－EA＝EB－EC，即AD＝CB．

    图②中EA－ED＝EC－EB，即AD＝CB．

    又∵∠DAB＝∠BCD，∠AOD＝∠COB，

    ∴△AOD≌△COB．

    数学老师的观点：

    （1）数学老师说：小明添加的条件是错误的，请你给出解释．

    你的想法：

    （2）请你重新添加一个满足问题要求的条件

    ，并说明理由．

     

    查看答案和解析>>

    同步练习册答案