
 经过圆心O时,求
经过圆心O时,求 的长;
的长; 所在圆的圆心O′到弦AB的距离;
所在圆的圆心O′到弦AB的距离; 与
与 所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值; 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点.试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点.试探究四边形OMPN的形状,并证明你的结论.
 解:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE
解:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE =
= =
= ;
;
 折叠前后所在的⊙O与⊙O′是等圆,
折叠前后所在的⊙O与⊙O′是等圆, ;
; 与
与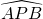 所在圆外切于点P时,
所在圆外切于点P时,
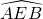 于点E,交
于点E,交 于点F,
于点F, ,
, ;
; 证明如下:
证明如下: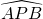 和
和 所在圆的圆心,
所在圆的圆心, 所在圆外切,
所在圆外切, 所在圆与⊙O都是等圆,
所在圆与⊙O都是等圆, ;
; 的圆心角,再根据弧长公式计算即可;
的圆心角,再根据弧长公式计算即可; 所在圆的圆心O′到弦AB的距离;
所在圆的圆心O′到弦AB的距离; 与
与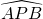 所在圆外切于点P时,过点O作EF⊥AB交
所在圆外切于点P时,过点O作EF⊥AB交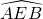 于点E,交
于点E,交 于点F,根据垂径定理及折叠,可求点O到AB、CD的距离之和;
于点F,根据垂径定理及折叠,可求点O到AB、CD的距离之和;

科目:初中数学 来源: 题型:
 |
| AB |
 |
| AB |
 |
| AOB |
 |
| AB |
 |
| CD |
 |
| AB |
 |
| CD |

查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
 |
| AB |
 |
| AB |
 |
| CD |
 |
| AB |
 |
| CD |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(带解析) 题型:解答题
已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的 经过圆心为O时,求
经过圆心为O时,求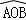 的长度;
的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的 与
与 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的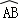 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.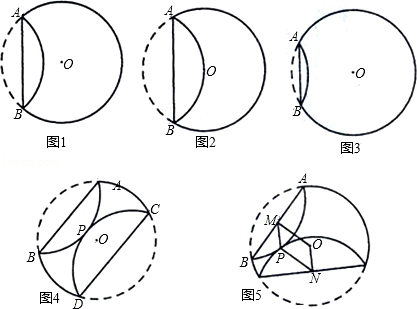
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
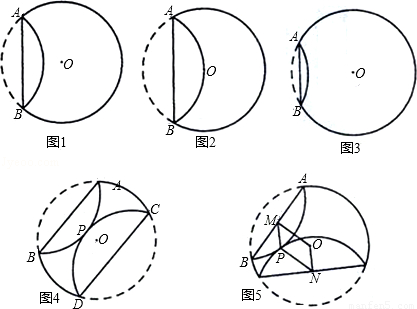
已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的 经过圆心为O时,求
经过圆心为O时,求 的长度;
的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的 与
与 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012年江西省南昌市中考数学试卷(解析版) 题型:解答题
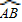 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;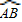 经过圆心为O时,求
经过圆心为O时,求 的长度;
的长度; 与
与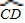 所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值; 与
与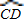 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com