
�����߶�a=5��b=3��c��ֵΪ��������a��b��cΪ�߿���������Σ�������
A. 1�� B. 3�� C. 5�� D. ������
C �����������������ε����߹�ϵ�ɵ�5-3��c��5+3����2��c��8����c��ֵΪ����������cΪ3��5��7�����ɵ���a��b��cΪ�߿���������εĸ���Ϊ3������ѡB.�������ĸ���ͨ��־ͼ�У�����Գ�ͼ�ε��ǣ�������
A.  B.
B.  C.
C.  D.
D. 
��֪ʵ��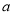 ��
�� 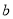 ���㣺
���㣺 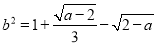 ����
����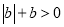 ����
����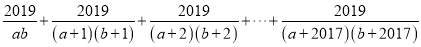 ��ֵ��
��ֵ��
��֪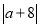 ��
��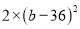 ��Ϊ�෴������
��Ϊ�෴������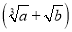 ��ƽ������
��ƽ������
�Ķ��������Ϣ���ش����⣺
�������ϣ����ǰѵ������������ȵĵ㣬������������ġ��е㡱�����磺
�ٱ�ʾ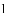
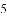
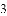
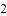
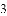
�ڱ�ʾ


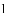

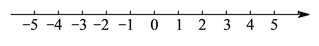
��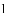

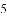
��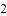


��֪ʵ��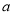 ��
�� 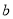 ��
�� 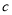 ���㣺
���㣺 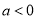 ��
�� 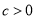 ��
�� 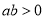 ����
����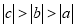 ��
��
��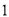 ���������ϱ����ʾ
���������ϱ����ʾ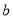 ��
�� 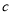 �ĵ�Ĵ���λ�ã�
�ĵ�Ĵ���λ�ã�
��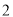 ������
������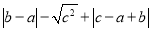 ��
��

 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�²� ��ĩ���� ���ͣ������
ij�̳�Ϊ����������Ĺ˿�,������һ���齱�,���涨:�˿�ÿ����100Ԫ��Ʒ,���ܻ��һ�γ齱�Ļ���.�齱��������:�ڳ齱����,��100������,�ֱ�д��1,2,3,��,100��100������,�鵽ĩλ����5�Ŀɻ�20Ԫ����ȯ,�鵽������88�Ŀɻ�200Ԫ����ȯ,�鵽66��99�Ŀɻ�100Ԫ����ȯ.ij�˿�������130Ԫ,����ù���ȯ�ĸ����Ƕ���?�����20Ԫ��100Ԫ��200Ԫ����ȯ�ĸ��ʷֱ��Ƕ���?
P(��ù���ȯ)= ��P(���20Ԫ����ȯ)= ��P(���100Ԫ����ȯ)= ��P(���200Ԫ����ȯ)= �������������������������¼����ʴ�С���������㣺�ٷ��������������Ŀ����ȫ����������������ߵı�ֵ�����䷢���ĸ��ʵĴ�С�� ����������˿͵����Ѷ���100Ԫ��200Ԫ֮��,��˿��Ի��һ�γ齱�Ļ���. �ڳ齱����,д��66,88,99�����Ӹ���1��,ĩλ������5����...����С��������ɵ�L�ε�ͼ����,�����ֲ�ͬ�ķ�������һ��С������,ʹ����Ϊ��Գ�ͼ��.
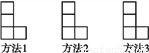
��ͼ��,ͼ��,ͼ��,ͼ��,��,����Χ�����Ӱ���ij�ֹ��ɰڳɵ�һ�С��㡱��,�������ֹ��ɰ�.
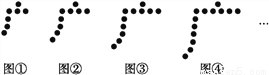
(1)��5�����㡱���е����Ӹ���������������.
(2)��n�����㡱����Ҫ����ö����?
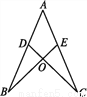
�鿴����ͼ,��D��AB��,��E��AC��,AB=AC,AD=AE.��˵����B=��C.
�Ȼ�������ֵ:(a-2)2-(a-1)��(a+1)+5a,����a=-2.
�鿴��С�Ϻ�С����ͬһ��·ͬʱ��ѧУ������ijͼ��ݲ�������,ѧУ��ͼ��ݵ�·����4 km,С�������г�,С������,��С�ϴ�ԭ·�ص�ѧУʱ,С���պõ���ͼ���,ͼ������O��A��B��C���߶�OD�ֱ��ʾ������ѧУ��·��s(km)����������ʱ��t(min)֮��Ĺ�ϵ,�����ͼ��ش�:�����ĸ�����
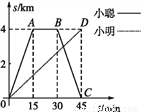
��С����ͼ��ݲ������ϵ�ʱ��Ϊ15 min;
��С�Ϸ���ѧУ���ٶ�Ϊ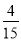 km/min;
km/min;
��С���뿪ѧУ��·��s(km)����������ʱ��t(min)֮��Ĺ�ϵʽ��s=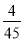 t;
t;
�ܵ�С����С��ӭ������ʱ,������ѧУ��·����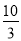 km.
km.
������ȷ���۵������_____.
�鿴�� �������� Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������³�������·���ʵ��2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����֪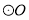 �İ뾶
�İ뾶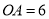 ��
�� 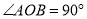 ����
����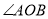 ���ԵĻ�
���ԵĻ�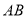 �ij�Ϊ�� ��
�ij��� ��
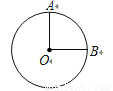
A. 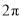 B.
B. 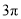 C.
C. 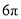 D.
D. 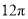
��ͼ�� 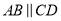 ��
�� 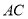 ��
�� 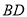 ����
����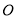 ��
�� 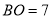 ��
�� 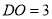 ��
�� 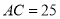 ����
����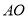 ���� ����
���� ����
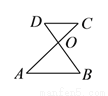
A. 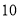 B.
B. 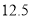 C.
C. 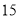 D.
D. 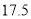
��������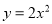 ������ƽ��һ����λ��������ƽ��һ����λ������ƽ�ƺ�õ��������߽���ʽΪ�� ����
������ƽ��һ����λ��������ƽ��һ����λ������ƽ�ƺ�õ��������߽���ʽΪ�� ����
A. 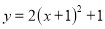 B.
B. 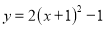 C.
C. 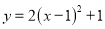 D.
D. 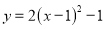
�����κ���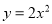 ��ͼ����
��ͼ����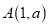 ����
����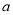 ��ֵΪ�� ����
��ֵΪ�� ����
A. 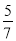 B.
B. 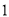 C.
C. 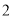 D.
D. 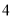
��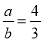 ����
����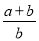 ��ֵ���ڣ� ����
��ֵ���ڣ� ����
A. 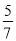 B.
B. 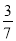 C.
C. 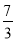 D.
D. 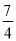
�����������
ѧϰ��������ȫ�ȵ��ж�����������SSS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ����ԡ������������������ߺ�����һ�ߵĶԽǶ�Ӧ��ȡ������ν����о���
������˼����
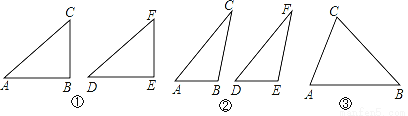
���Dz����������÷������Ա�ʾΪ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E��Ȼ�ԡ�B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ���ǡ������������̽����
������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
��ͼ�٣��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E=90�㣬������ ��������֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��ͼ�ڣ��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E���Ƕ۽ǣ�����֤������ABC�ա�DEF����ʾ������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H����
���������������B�����ʱ����ABC�͡�DEF��һ��ȫ�ȣ�
�ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ���������ͼ�ۣ���ͼ�����ó߹�������DEF��ʹ��DEF�͡�ABC��ȫ�ȣ�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ˮ��2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����֪��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD�ӳ����ϵ�һ�㣬BE=BA��������ۣ��١�ABD�ա�EBC����AC=2CD����AD=AE=EC���ܡ�BCE+��BCD=180�㣮������ȷ���ǣ�������
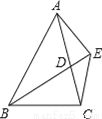
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
C ����������֪BDΪ��ABC�Ľ�ƽ���ߣ����ݽ�ƽ���ߵĶ���ɵá�ABD=��CBD���ڡ�ABD�͡�EBC�У�BD��BC����ABD����CBD��BE��BA����SAS���ж���ABD�ա�EBC�����ɵâ���ȷ��������֪��������֤��AC=2CD���ڴ��� ��֪BDΪ��ABC�Ľ�ƽ���ߣ�BD=BC��BE=BA���ɵá�BCD=��BDC=��BAE=��BEA�� ���ɡ�BCE=��BDA����BCE=��BCD+��D...��֪���ڡ�ABC�У���A=60�㣬��Ҫ�ж���ABC�ǵȱ������Σ���������һ��������������������˵����
���������������AB=AC������ô��ABC�ǵȱ������Σ�
�����������������B=��C������ô��ABC�ǵȱ������Σ�
�����������������AB��BC�ϵĸ���ȡ�����ô��ABC�ǵȱ������Σ�
����˵���У���ȷ���У�������
A. 3�� B. 2�� C. 1�� D. 0��
�鿴����ͼ������֪�ġ�ABC�У������²�����ͼ��
�ٷֱ���B��CΪԲ�ģ��Դ���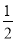 BC�ij�Ϊ�뾶�����������ཻ������M��N��
BC�ij�Ϊ�뾶�����������ཻ������M��N��
����ֱ��MN��AB�ڵ�D������CD��
��CD=AC����A=50�㣬���ACB�Ķ���Ϊ��������
A. 90�� B. 95�� C. 100�� D. 105��
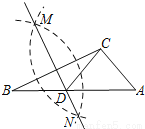
�鿴����ͼ���ڡ�ABC�У�AB=AC��DΪBC��һ�㣬��DA=DC��BD=BA�����B�Ĵ�СΪ
A. 40�� B. 36�� C. 30�� D. 25��
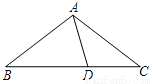
�鿴����ͼ,��ABC�ա�AEF,AB=AE,��B=��E,����ڽ���:��AC=AF;�ڡ�FAB=��EAB;��EF=BC;�ܡ�EAB=��FAC.������ȷ���۵ĸ�����(����)
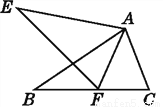
A. 1�� B. 2�� C. 3�� D. 4��
�鿴����ƽ��ֱ������ϵ�У���P��1����2������x��ԳƵĵ�������ǣ�������
A. ��1��2�� B. ����1����2�� C. ����1��2�� D. ����2��1��
�鿴�� �������� Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ˮ��2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���������У������ж�����ֱ��������ȫ�ȵ��ǣ�������
A. ��ֱ�DZ߶�Ӧ��� B. б�ߺ�һ��ֱ�DZ߶�Ӧ���
C. ����Ƕ�Ӧ��� D. һ����Ǻ�б�߶�Ӧ���
C ��������Aѡ��ɡ���ֱ�DZ߶�Ӧ��ȡ����ݡ�SAS����֤����ֱ��������ȫ�ȣ� Bѡ��ɡ�б�ߺ�һֱ�DZ߶�Ӧ��ȡ����ݡ�HL����֤����ֱ��������ȫ�ȣ� Cѡ��ɡ�����Ƕ�Ӧ��ȡ�����֤����ֱ��������ȫ�ȣ���Ϊ֤��������ȫ�ȣ�������Ҫһ���߶�Ӧ��ȣ� Dѡ��ɡ�һ����Ǻ�б�߶�Ӧ��ȡ����ݡ�AAS����֤����ֱ��������ȫ�ȣ� ��ѡC.һ������ε��ڽǺͱ�������Ǻ͵�2������180�㣬�������εı���Ϊ��������
A. 7 B. 8 C. 9 D. 10
�鿴��һ�����ǰ���ͼ������һ����ͼ�СϦ��Ķ���Ϊ��������
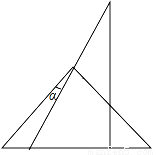
A. 35�� B. 30�� C. 25�� D. 15��
�鿴����ͼ��EA��DF��AE=DF��Ҫʹ��AEC�ա�DFB��ֻҪ��������
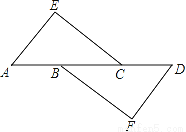
A. AB=CD B. EC=BF C. ��A=��D D. AB=BC
�鿴����ͼ����֪�ڡ�ABC�У���ABC=70�㣬��C=50�㣬BD�ǽ�ƽ���ߣ����BDC�Ķ���Ϊ
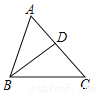
A. 95�� B. 100�� C. 110�� D. 120��
�鿴�������߶�a=5��b=3��c��ֵΪ��������a��b��cΪ�߿���������Σ�������
A. 1�� B. 3�� C. 5�� D. ������
�鿴�� �������� Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ� ������ һԪһ�η��� 5��1����ʶһԪһ�η��� ͬ�����Ծ� ���� ���ͣ������
����x��40%��6������13���÷��̱�ʾΪ______________��
40%x��6��13 ����������Ϊ��x��40%��6������ʾΪ:40%x+6,���Ը���������г�������: 40%x+6=13,�ʴ�Ϊ: 40%x+6=13.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ� ������ һԪһ�η��� 5��1����ʶһԪһ�η��� ͬ�����Ծ� ���� ���ͣ���ѡ��
���������е�Ӱ�죬����4�·ݼ��ļ۸����δ���½�����ԭ��ÿ��12Ԫ���������ν���a%���ۼ��µ���ÿ��5Ԫ���������еķ�������ȷ����(����)
A. 12(1��a%)2��5 B. 12(1��a%)2��5 C. 12(1��2a%)��5 D. 12(1��a2%)��5
B ����������Ϊԭ��ÿ��12Ԫ,��һ�ν���a%��۸�Ϊ:12(1��a%)Ԫ,�ڶ����ڵ�һ�ν��۵Ļ������ֽ���a%,���Եڶ��ν��ۺ�۸�Ϊ:12(1��a%)(1��a%),��Ϊ,���Կ��з���Ϊ: ,��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ� ������ ��ʽ����Ӽ� 3��3����ʽ ͬ�����Ծ� ���� ���ͣ���ѡ��
��3m��2��x2yn��1�ǹ���x��y����ε���ʽ����ϵ��Ϊ1����m��n��ֵ�ֱ��ǣ�������
A. 1��4 B. 1��2 C. 0��5 D. 1��1
B ��������������ã� �����. ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���ѧ���꼶�²ᣨ����ר�棩 �����ۺϼ�� ���ͣ���ѡ��
��ͼ��ʾ,ֱ��AB,CD�ཻ�ڵ�E,DF��AB.����AEC=100��,���D���� (����)
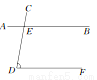
A. 70�� B. 80�� C. 90�� D. 100��
B ���������ߡ�CEA=100�㣬 ���CEB=180��?��CEA=80�㣻 �֡�AB��DF�� ���CEB=��D=80�㣻 �ʴ�Ϊ��B.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com