
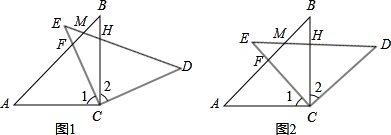
如图1,在△ABC和△PQD中,AC = k BC,DP = k DQ,∠C =∠PDQ,D、E分别是AB、AC的中点,点P在直线BC上,连结EQ交PC于点H.
猜想线段EH与AC的数量关系,并证明你的猜想.

结论:EH=![]() AC.
AC.
证明:取BC边中点F,连接DE、DF
∵D、E、F分别是边AB、AC、BC的中点.
∴DE∥BC且DE=![]() BC,
BC,
DF∥AC且DF=![]() AC,
AC,
EC=![]() AC ∴四边形DFCE是平行四边形.
AC ∴四边形DFCE是平行四边形.
∴∠EDF=∠C.
∵∠C=∠PDQ,∴∠PDQ =∠EDF , ∴∠PDF=∠QDE.
又∵AC=kBC,∴DF=kDE.
∵DP=kDQ ,∴![]() .
.
∴△PDF∽△QDE.
∴∠DEQ=∠DFP.
又∵DE∥BC,DF∥AC, ∴∠DEQ=∠EHC,∠DFP=∠C.
∴∠C =∠EHC.
∴EH=EC.
∴EH=![]() AC.
AC.
选图2.结论:EH=![]() AC.
AC.
证明:取BC边中点F,连接DE、DF.
∵D、E、F分别是边AB、AC、BC的中点,
∴DE∥BC且DE=![]() BC, DF∥AC且DF=
BC, DF∥AC且DF=![]() AC,
AC,
EC=![]() AC ,∴四边形DFCE是平行四边形.
AC ,∴四边形DFCE是平行四边形.
∴∠EDF=∠C.
∵∠C=∠PDQ,∴∠PDQ=∠EDF , ∴∠PDF=∠QDE.
又∵AC=BC, ∴DE=DF,∵PD=QD,∴△PDF≌△QDE.
∴∠DEQ=∠DFP.
∵DE∥BC,DF∥AC, ∴∠DEQ=∠EHC,∠DFP=∠C.
∴∠C =∠EHC
∴EH=EC.
∴EH=![]() AC.
AC.
选图3. 结论: EH=![]() AC.
AC.
证明:连接AH.
∵D是AB中点,∴DA=DB.
又∵DB=DQ,∴DQ=DP=AD.∴∠DBQ=∠DQB,.
∵∠DBQ+∠DQB+∠DQA+∠DAQ,=180°,∴∠AQB=90°,
∴AH⊥BC.
又∵E是AC中点,∴HE=![]() AC.
AC.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com