解:(1)∵Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,
∴AB=

=

=10(cm);
∴AB的长为10cm;
(2)①∵EF∥AB,
∴△CEF∽△CAB,
∴
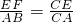
,
∵点E出发x秒后,AE=2xcm,CE=8-2x(cm),
又∵线段EF的长为ycm,
∴
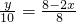
,
∴y=-

x+10;
∴y与x的函数关系式为y=-

x+10(0<x<4);
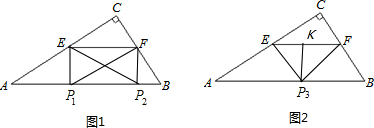
②存在.
过点E作EP⊥AB于P,当EP=EF时,
△PEF是等腰直角三角形,
∵sin∠A=
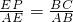
,
即:
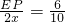
,
∴EP=

x,
∴

x=-

x+10,
解得:x=
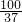
;
同理:当FP⊥AB于P,FP=EF时,△PEF是等腰直角三角形,此时,x=
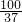
;
当EF的中垂线PK交AB于P,交EF于K,且EF=2PK时,△PEF是等腰直角三角形,
同理可求得:KP=

x,
∴2×

x=-

x+10,
解得:x=

.
∴存在这样的点共三个.
分析:(1)由在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,根据勾股定理即可求得AB的长;
(2)①由EF∥AB,可得△CEF∽△CAB,又由点E出发x秒后,线段EF的长为ycm,求得AE与EC的长,然后根据相似三角形的对应边成比例,即可求得y与x的函数关系式;
②分别从当∠PEF=90°,∠PFE=90°与∠EPF=90°去分析求解,利用三角函数的知识即可求得相应的x的值.
点评:此题考查了勾股定理,相似三角形的判定与性质以及等腰直角三角形性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想,方程思想与分类讨论思想的应用.


 =
= =10(cm);
=10(cm);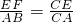 ,
,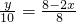 ,
, x+10;
x+10; x+10(0<x<4);
x+10(0<x<4);
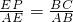 ,
,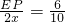 ,
, x,
x, x=-
x=- x+10,
x+10,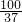 ;
;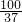 ;
; x,
x, x=-
x=- x+10,
x+10, .
.

 (1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=
(1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=