

| 解:(1)B与A(1,0)关于原点对称, ∴B(-1,0), ∵y=x+b过点B, ∴-1+b=0,b=1, ∴y=x+1, 当y=4时,x+1=4,x=3, ∴D(3,4); (2)作DE⊥x轴于点E,则OE=3,DE=4, ∴  , ,若△POD为等腰三角形,则有以下三种情况, ①以O为圆心,OD为半径作弧交x轴的正半轴于点P1,则OP1=OD=5, ∴P1(5,0); ②以D为圆心,DO为半径作弧x轴的正半轴于点P2,则DP2=DO=5, ∵DE⊥OP2, ∴P2E=OE=3, ∴OP2=6, ∴P2(6,0); ③取OD的中点K,过K作OD的垂线交x轴的正半轴于点P3,则OP3=DP3,易知△OKP3∽△DCO, ∴  , ,∴  , ,∴  , ,综上所述,符合条件的点P有三个,分别是P1(5,0),P2(6,0); (3)①当P1(5,0)时,P1E=OP1-OE=5-3=2,DE=4, ∴  , ,⊙P的半径为  , ,∵⊙O与⊙P外切, ∴⊙O的半径为5-  ; ;②当P2(6,0)时,P2D=DO=5,OP2=6, ∴⊙P的半径为5, ∵⊙O与⊙P外切, ∴⊙O的半径为1; ③当  时,P3D=OP3= 时,P3D=OP3= , ,∴⊙P的半径为  , ,∵⊙O与⊙P外切, ∴⊙O的半径为O,即此时⊙O不存在。 |
 |


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
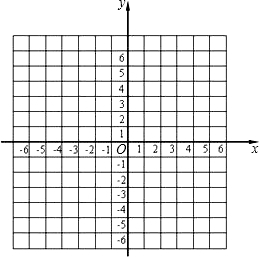 在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.查看答案和解析>>
科目:初中数学 来源: 题型:
A、(-1,
| ||
B、(-1,-
| ||
C、(-
| ||
D、(-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com