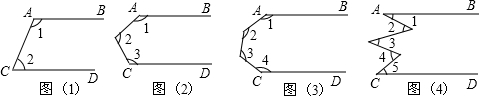
解:(1)∵AB∥CD,
∴∠1+∠2=180°;

(2)过∠2的顶点作EF∥AB,则EF∥CD,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠AEF+∠FEC+∠3=180°+180°,
即,∠1+∠2+∠3=360°;
(3)过∠2、∠3的顶点分别作EF∥AB,GH∥AB,则AB∥EF∥GH∥CD,
∴∠1+∠AEF=180°,∠FEG+∠EGH=180°,∠HGC+∠4=180°,
∴∠1+∠AEF+∠FEG+∠EGH+∠HGC+∠4=180°×3,
即,∠1+∠2+∠3+∠4=540°;
(4)过∠2、∠3、∠4的顶点作EF∥AB,GH∥AB,MN∥AB,则AB∥EF∥GH∥MN∥CD,
∴∠1=∠AEF,∠FEG=∠EGH,∠HGM=∠GMN,∠NMC=∠5,
∴∠AEF+∠FEG+∠GMN+∠NMC=∠1+∠EGH+∠HGM+∠5,
即∠2+∠4=∠1+∠3+∠5.
分析:(1)根据两直线平行,同旁内角互补解答即可;
(2)过∠2的顶点作AB的平行线,再利用两直线平行,同旁内角互补解答即可;
(3)过∠2、∠3的顶点作AB的平行线,再利用两直线平行,同旁内角互补解答即可;
(4)过∠2、∠3、∠4的顶点作AB的平行线,再利用两直线平行,内错角相等进行解答即可.
点评:本题主要考查了两直线平行同旁内角互补,两直线平行,内错角相等的性质,过角的顶点作AB的平行线,构造出同旁内角或内错角是解题的关键,此题规律性较强,需熟练掌握.