
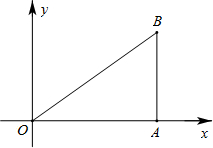
 个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.
个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.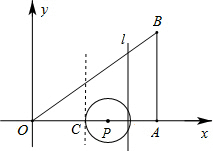 解:(1)当P在线段OA上运动时,OP=3t,AC=t,
解:(1)当P在线段OA上运动时,OP=3t,AC=t, ,
, <t<
<t< ;
; =
=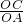 ,即
,即 =
= ,
, (4-t),
(4-t), (4-t)=7-3t,
(4-t)=7-3t, ,
, 时,
时,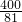 ,PC2=(7-3t)2=
,PC2=(7-3t)2= ,
, (4-t+a),由CD=PB,得
(4-t+a),由CD=PB,得 (4-t+a)=7-3t,
(4-t+a)=7-3t,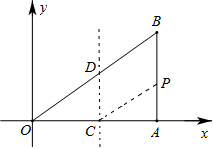
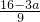 ,
, =
= ,即AB•PC=OB•AP,
,即AB•PC=OB•AP, (4-t+a)=5×(3t-4),
(4-t+a)=5×(3t-4),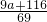 ,
,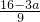 =
=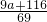 ,
, ,即直线l比P点迟
,即直线l比P点迟 秒出发.
秒出发.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
 =2,∠ADC=30°
=2,∠ADC=30°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com