
分析 (1)首先计算乘方,然后从左向右依次计算即可.
(2)首先计算乘方,然后计算乘法和除法即可.
(3)首先计算计算乘方和乘法,然后计算减法即可.
(4)根据平方差公式计算即可.
解答 解:(1)(-1)2012+(-$\frac{1}{2}$)-2-(3.14-π)0
=1+4-1
=4
(2)$\frac{1}{4}$a2b•(-2ab2)2÷(-$\frac{1}{2}$a4b5)
=$\frac{1}{4}$a2b•4a2b4÷(-$\frac{1}{2}$a4b5)
=a4b5÷(-$\frac{1}{2}$a4b5)
=-2
(3)(2a+3b)(2a-3b)-(a-3b)2
=4a2-9b2-a2+6ab-9b2
=3a2-18b2+6ab
(4)(x-y-z)(x+y+z)
=x2-(y+z)2
=x2-y2-z2-2yz
点评 此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
 计算:如图,在Rt△ABC中,∠ACB=90°.
计算:如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求∠BAD的度数与AD的长.
已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求∠BAD的度数与AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
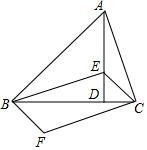 如图,在△ABC中,AD⊥BC于点D,∠ABD=45°,在AD上取一点E,连接BE,使得BE=AC,连接CE,将线段CA绕点C逆时针旋转90°,到达CF的位置,连接BF.已知∠CAD=∠BCF.
如图,在△ABC中,AD⊥BC于点D,∠ABD=45°,在AD上取一点E,连接BE,使得BE=AC,连接CE,将线段CA绕点C逆时针旋转90°,到达CF的位置,连接BF.已知∠CAD=∠BCF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com