
给出下列命题,正确的
①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等; ③等腰三角形最小边是底边;④等边三角形的高、中线、角平分线都相等;⑤等腰三角形都是锐角三角形
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】【解析】 ①等腰三角形的顶角的角平分线、底边上的中线和高重合,故本选项错误; ②等腰三角形两腰上的高相等,正确; ③等腰三角形的最小边不一定是底边,故本选项错误; ④等边三角形的高、中线、角平分线都相等,正确; ⑤等腰三角形不一定是锐角三角形,故本选项错误; 其中正确的有2个,故选B.科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
在下列图形中,不能折成正方体的是( ).
A. 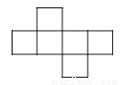 B.
B. 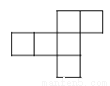 C.
C. 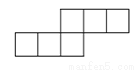 D.
D. 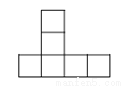
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若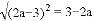 ,则
,则
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:解答题
如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.
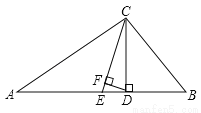
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:填空题
已知命题“如果一个四边形是平行四边形,那么这个四边形是旋转对称图形.”,写出它的逆命题是 ,该逆命题是 命题(填“真”或“假”).
如果一个四边形是旋转对称图形,那么这个四边形是平行四边形,真. 【解析】试题分析: “如果一个四边形是平行四边形,那么这个四边形是旋转对称图形”的逆命题是“如果一个四边形是旋转对称图形,那么这个四边形是平行四边形”.该逆命题是真命题.查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:单选题
下列命题是假命题的是( )
A. ?如果a∥b,b∥c,那么a∥c
B. 锐角三角形中最大的角一定大于或等于60°
C. 两条直线被第三条直线所截,内错角相等
D. 矩形的对角线相等且互相平分
C 【解析】试题分析:依次分析各选项即可得到结论. A.如果a∥b,b∥c,那么a∥c,B.锐角三角形中最大的角一定大于或等于60°,D.矩形的对角线相等且互相平分,均是真命题,不符合题意; C.两条直线被第三条直线所截,若这两条直线平行,则内错角相等,故是假命题.查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:解答题
2017年4月23日是 “世界读书日”,宜宾市某中学举行“多读书,读好书”活动,对学生的课外读书时间进行了随机问卷调查,用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题:
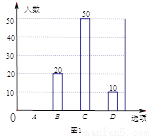
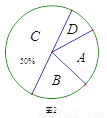
(1)本次接受问卷调查的学生共有________人,在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,则该校学生课外读书时间在“A”选项的约有_____人.
100 10% 72 240 【解析】试题分析: (1)由两幅统计图可知,B选项有50人,占被调查总数的50%,由此即可计算接受调查的学生数为100人,结合D选项有10人可计算出在扇形统计图中D选项所占的百分比为10%; (2)结合图形统计图中的信息和(1)中的计算结果,可得扇形统计图中B选项所对应的圆心角为:360°×20%=72°; (3)由(1)中所得接受调查的总人数...查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:单选题
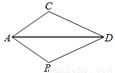
如图,已知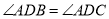 ,则不一定能使
,则不一定能使 的条件是(??)
的条件是(??)
A. 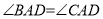 B.
B. 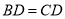 C.
C. 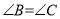 D.
D. 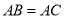
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:单选题
矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )
A. 57.5° B. 32.5° C. 57.5°,23.5° D. 57.5°,32.5°
D 【解析】【解析】 ∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC,AB∥CD,AC=BD,AO=OC,OB=OD,∴OB=OA=OC=OD,∠OAB=∠OCD,∠DAO=∠OCB,∴∠OAD=∠ODA,∠OCB=∠OBC,∠ODC=∠OCD,∠OAB=∠OBA=×(180°﹣∠AOB)=×(180°﹣65°)=57.5°,∵∠ABC=90°,∴∠ACB=90°﹣57.5°=32...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com