练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某检修小组乘一辆检修车沿铁路检修，规定向东走为正，向西走为负，小组的出发地记为0，某天检修完毕时，行走记录（单位：千米）如下：

    +10，-2，+3，-1，+9，-3，-2，+11，+3，-4，+6．

    （1）问收工时，检修小组距出发地有多远？在东侧还是西侧？

    （2）若检修车每千米耗油2.8升，求从出发到收工共耗油多少升？

    （1）30千克；（2）151.2升. 【解析】试题分析：本题考查了正负数，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示． （1）求得记录的数的和，根据结果即可确定所处的位置； （2）求得记录的数的绝对值的和，乘以2．8即可求解． 试题解析： （1）10-2+3-1+9-3-2+1...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省南京市建邺区2016－2017学年度第一学期期末调研测试九年级数学试卷 题型：填空题

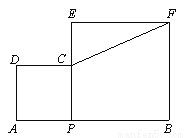
    如图，AB＝5，P是线段AB上的动点，分别以AP、BP为边，在线段AB的同侧作正方形APCD和正方形BPEF，连接CF，则CF的最小值是____．

    【解析】设AP=x,则BP=5－x,所以EF=BP=5－x,EC=5－x－x=5－2x,在直角三角形EFC中,根据勾股定理可得: ,当x=3时,CF有最小值,CF最小值为,故答案为: .

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型：解答题

    如图，一次函数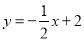分别交y轴、x 轴于A、B两点，抛物线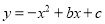过A、B两点.

    （1）求这个抛物线的解析式；

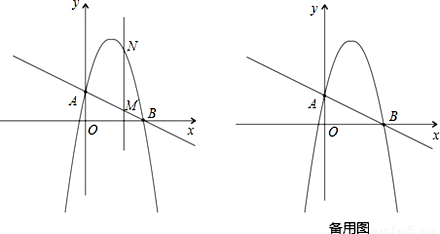
    （2）作垂直x轴的直线x=t，在第一象限交直线AB于点M，交这个抛物线于点N.求当t 取何值时，MN有最大值？最大值是多少？

    （3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标.

    （1）抛物线解析式为 ； （2）当 t=2 时，MN有最大值为 4； （3）D（0，6）或（0，-2）或（4，4）. 【解析】试题分析： （1）先由直线分别交y轴、x轴于点A、B这一条件求出点A、B的坐标，将所求坐标代入抛物线列出关于的值即可得到所求抛物线的解析式； （2）如图1，由题意可知点M的横坐标为t，根据点M在直线上，点N在（1）中所求抛物线上，可用含“t”的...

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型：单选题

    如图，在⊙O中，半径为13，弦AB垂直于半径OC交OC于点D，AB=24，则CD的长为（ ）

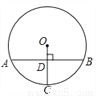
    A. 5 B. 12 C. 8 D. 7

    C 【解析】连接OA. ∵弦AB垂直于半径OC, ∴AD= . ∵半径为13， ∴OA=OC=13. 由勾股定理得 , ∴CD=OC-OD=13-5=8. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型：单选题

    下列事件中是必然事件的是（ ）

    A. 打开电视，它正在播广告 B. 掷两枚质地均匀的骰子，点数之和一定大于6

    C. 某射击运动员射击一次，命中靶心 D. 早晨的太阳从东方升起

    D 【解析】A. 打开电视，它正在播广告是随机事件; B. 掷两枚质地均匀的骰子，点数之和一定大于6是不可能事件; C. 某射击运动员射击一次，命中靶心是随机事件; D. 早晨的太阳从东方升起是必然事件; 故选D.

    查看答案和解析>>

    科目：初中数学 来源：山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    在数轴上与-3的距离等于4的点表示的数是  

    -7 、1 【解析】【解析】 数轴上与3距离等于4个单位的点有两个， 从表示的点向左数4个单位是， 从表示的点向右数4个单位是． 故答案为：．

    查看答案和解析>>

    科目：初中数学 来源：山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    若│a∣= —a ,则a是（ ）.

    A. 非负数 B. 非正数 C. 正数 D. 负数

    B 【解析】 本题考查绝对值的性质。绝对值是非负的，故—a ≥0即a≤0，a为非正数。

    查看答案和解析>>

    科目：初中数学 来源：北京市顺义区2018届初三上学期期末考试数学试卷 题型：解答题

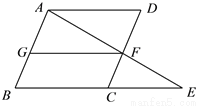
    如图，E是□ABCD的边BC延长线上一点，AE交CD于点F，FG∥AD交AB于点G．

    （1）填空：图中与△CEF相似的三角形有__________；（写出图中与△CEF相似的所有三角形）

    （2）从（1）中选出一个三角形，并证明它与△CEF相似．

    △ADF，△EBA，△FGA； 【解析】试题分析：（1）由四边形ABCD是平行四边形，可得AB∥CD，AD∥BC，平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似，即可得； （2）根据∠DAF=∠E，∠FCE=∠D，即可证明△ADF∽△ECF. 试题解析：（1）△ADF，△EBA，△FGA； （2）△ADF∽△ECF， ∵四边形ABCD为平行四边形...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年陕西安市九年级（上）期末数学试卷 题型：单选题

    如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，，④360°﹣α﹣β，∠AEC的度数可能是（　　）

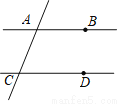
    A. ①②③ B. ①②④ C. ①③④ D. ①②③④

    B 【解析】试题解析：点有4种可能位置． （1）如图，由∥ 可得 （2）如图，过 作平行线，则由∥可得 （3）如图，由∥可得 （4）如图，由∥可得 的度数可能为 故选：D．

    查看答案和解析>>

    同步练习册答案