练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

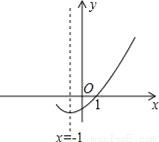
    如图，是二次函数 y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c=0；②b＞2a；③ax2+bx+c=0的两根分别为﹣3和1；④a﹣2b+c＞0．其中正确的命题是（　　）

    A. ①② B. ②③ C. ①③ D. ①②③④

    C 【解析】∵x＝1时，y＝0，∴a＋b＋c＝0，所以①正确；∵x＝＝－1，∴b＝2a，所以②错误；∵点(1，0)关于直线x＝－1对称的点的坐标为(－3，0)，∴抛物线与x轴的交点坐标为(－3，0)和(1，0)，∴ax2＋bx＋c＝0的两根分别为－3和1，所以③正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，而a＋b＋c＝0，b＝2a，∴c＝－3a，∴a－2b＋c＝－3b，∵b＞0，∴－3b...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西省2018届九年级上期末模拟数学试卷 题型：单选题

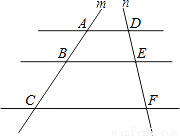
    如图，AD∥BE∥CF，直线m，n与这三条平行线分别交于点A、B、C和点D、E、F，已知AB=5，BC=10，DE=4，则EF的长为（   ）

    A. 12.5                                          B. 12                                          C. 8                                          D. 4

    C 【解析】试题解析：∵AD∥BE∥CF， ∴，即， 解得，EF=8， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市费县2017-2018学年八年级（上）期中数学试卷 题型：解答题

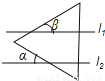
    如图，已知直线l1∥l2，将等边三角形如图放置，若∠α=40°，则∠β等于______．

    20° 【解析】过点A作AD∥l1，如图， 则∠BAD=∠β. ∵l1∥l2， ∴AD∥l2， ∵∠DAC=∠α=40°. ∵△ABC是等边三角形， ∴∠BAC=60°， ∴∠β=∠BAD=∠BAC?∠DAC=60°?40°=20°. 故答案为：20°.

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：解答题

    设a，b是任意两个实数，规定a与b之间的一种运算“⊕”为：a⊕b= ，

    例如：1⊕（﹣3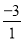）==﹣3，（﹣3）⊕2=（﹣3）﹣2=﹣5，（x2+1）⊕（x﹣1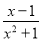）=（因为x2+1＞0），

    参照上面材料，解答下列问题：

    （1）2⊕4=　 　，（﹣2）⊕4=　 　；

    （2）若x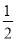＞ ，且满足（2x﹣1）⊕（4x2﹣1）=（﹣4）⊕（1﹣4x），求x的值．

    （1）2，﹣6；（2）x的值是3． 【解析】（1）2⊕4==2， （﹣2）⊕4=﹣2﹣4=﹣6； （2）∵x＞， ∴（2x﹣1）⊕（4x2﹣1）=（﹣4）⊕（1﹣4x）， 即=﹣4﹣（1﹣4x）， =4x﹣5， 4x2﹣1=（4x﹣5）（2x﹣1）， 4x2﹣1=4x2﹣14x+5， 2x2﹣7x+3=0， （2x﹣1）（x﹣3）=0， ...

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：填空题

    甲、乙两人分别从两地同时出发登山，甲、乙两人距山脚的竖直高度y（米）与登山时间x（分）之间的图象如图所示，若甲的速度一直保持不变，乙出发2分钟后加速登山，且速度是甲速度的4倍，那么他们出发_____分钟时，乙追上了甲．

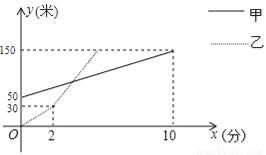
    【解析】试题解析：如图， ∵C（0，50），B（10，150）， ∴直线CD的解析式为y=10x+50， 由题意A（2，30）， 甲的速度为10米/分， ∴乙加速后的速度为40米/分， ∴乙从A到B的时间==3， ∴B（5，150）， ∴直线AB的解析式为y=40x-50， 由，解得 ∴那么他们出发分钟时，乙追上了甲．

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：单选题

    某商品原价200元，连续两次降价a%后售价为148元，下列所列方程正确的是（　　）

    A. 200（1+a%）2=148 B. 200（1﹣a%）2=148 C. 200（1﹣2a%）=148 D. 200（1﹣a2%）=148

    B 【解析】试题分析：主要考查增长率问题，本题可用降价后的价格=降价前的价格×（1-降价率），首先用x表示两次降价后的售价，然后由题意可列出方程．依题意得两次降价后的售价为200（1-a%）2，因此可得方程200（1-a%）2=148． 故选B

    查看答案和解析>>

    科目：初中数学 来源：北京师范大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦。我国西汉《周髀算经》中周公与商高对话中涉及勾股定理，所以这个定理也有人称商高定理，勾股定理在西方被称为毕达哥拉斯定理，相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。

    我们知道，可以用一个数表示数轴上的一个点，而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴，同时，增加一个垂直于x轴的数轴，叫做y轴，如下图。这样，我们可以用一组数对来表示平面上的一个点，同时，平面上的一个点也可以用一组数对来表示，比如下图中A点的位置可以表示为（2，3），而数对（2，3）所对应的点即为A。若平面上的点M 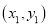，N 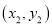，我们定义点M、N在x轴方向上的距离为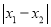： ，点M、N在y轴方向上的距离为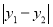： 。例如，点G（3，4）与点H（1，-1）在x轴方向上的距离为：|3-1|=2，点M、N在y轴方向上的距离为：|4-（-1）|=5。

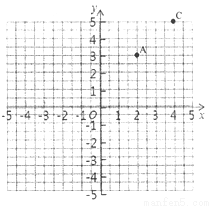
    （1）若点B位置为（-1，-1），请在图中画出点B；图中点C的位置用数对______来表示。

    （2）在（1）条件下，A、B两点在x轴方向上的距离为________，在y轴方向上的距离为_______，A、B两点间的距离为______；若E点、F点的位置分别为（a，b）、（c，d），点E、F之间的距离为|EF|，则=_______________。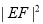

    （3）有一个点D，它与（0，0）点的距离为1，请画出D点所有可能的位置。

    （1）点C（4，5）；（2）3，4，5；（a-c）+（b-d）（3）见图中：圆. 【解析】试题分析：（1）根据有序数对的含义解答，明确有序数对前后两个数表示的含义； （2）根据两点在坐标轴方向的距离含义或解答；两点间的距离则根据勾股定理解答. （3）与（0，0）点的距离为1的点在以（0，0）为圆心，以1为半径的圆上. 【解析】 （1）点B的位置如图，点C的位置用数对（4，...

    查看答案和解析>>

    科目：初中数学 来源：北京师范大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    当x=_______时，代数式2x+1与5x-8的值相等.

    3 【解析】试题解析：根据题意列方程：2x+1=5x-8， 移项，合并同类项得 -3x=-9， 系数化为1，得x=3．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    下列说法正确的是( )

    A. 各边都相等的多边形叫正多边形 B. 圆上任意两点间的距离叫弧

    C. 三角形是多边形 D. 八边形有八个顶点，八个内角，八条对角线

    C 【解析】解：A．平面内，各边都相等，各角也相等的多边形叫正多边形，故A错误； B． 圆上任意两点间的部分叫弧，故B错误； C． 三角形是多边形，正确； D． 八边形有八个顶点，八个内角，20条对角线，故D错误． 故选C．

    查看答案和解析>>

    同步练习册答案