
分析 由点M关于y轴的对称点在第四象限内,即可得出关于k的一元一次不等式组,解之即可得出k的取值范围,再利用一次函数图象与系数的关系即可确定一次函数y=(k-2)x+k的图象经过的象限,此题得解.
解答 解:∵点M(k-2,k+1)关于y轴的对称点在第四象限内,
∴$\left\{\begin{array}{l}{k-2<0}\\{k+1<0}\end{array}\right.$,
∴k<-1.
∵在一次函数y=(k-2)x+k中,k-2<0,k<0,
∴一次函数y=(k-2)x+k的图象经过第二、三、四象限.
故答案为:一.
点评 本题考查了一次函数图象与系数的关系,熟练掌握“k<0,b<0?y=kx+b的图象在二、三、四象限”是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
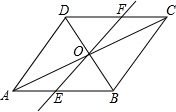 如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接DE、BF
如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接DE、BF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2 ).
如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2 ).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
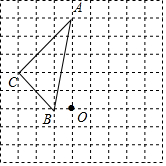 如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.
如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,过⊙O外一点P向⊙O作两条切线,切点分别为A、B,若⊙O的半径为2,∠APB=60°,则图中阴影部分的面积为4$\sqrt{3}$-$\frac{4}{3}$π.
如图,过⊙O外一点P向⊙O作两条切线,切点分别为A、B,若⊙O的半径为2,∠APB=60°,则图中阴影部分的面积为4$\sqrt{3}$-$\frac{4}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
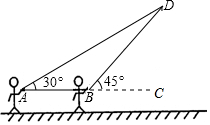 放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)
放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
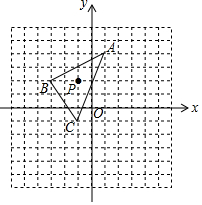 如图,△ABC中任意一点P(m,n),经过平移后对应点P1(m+4,n-3),将△ABC作同样的平移得到△A1B1C1,已知A(1,4)、B(-3,2),C(-1,-1).
如图,△ABC中任意一点P(m,n),经过平移后对应点P1(m+4,n-3),将△ABC作同样的平移得到△A1B1C1,已知A(1,4)、B(-3,2),C(-1,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com