练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，D为△ABC一点，AB=AC，BC=CD，∠ABD=15°，则∠A=________°．

    40
    分析：设∠A=x．根据三角形的外角的性质，得∠BDC=15+x，根据等腰三角形的性质，得∠CBD=∠CDB=15+x，则∠ABC=30+x，再根据等腰三角形的性质，得∠ACB=∠ABC=30+x，再根据三角形的内角和定理列方程求解．
    解答：设∠A=x．
    ∵BC=CD，∠ABD=15°，
    ∴∠CBD=∠CDB=15+x．
    ∵AB=AC，
    ∴∠ACB=∠ABC=30+x．
    ∴x+2（30+x）=180°，
    x=40°．
    即∠A=40°．
    点评：此题综合运用了等腰三角形的性质和三角形的内角和定理及其推论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    精英家教网认真阅读，并回答下面问题：
    如图，AD为△ABC的中线，S△ABD与S△ADC相等吗？（友情提示：S△表示三角形面积）
    解：过A点作BC边上的高h，
    ∵AD为△ABC的中线
    ∴BD=DC
    ∵S△ABD=
    1
    2
    BD•h    S△ADC=
    1
    2
    DC•h
    ∴S△ABD=S△ADC
    （1）用一句简洁的文字表示上面这段内容的结论：
     

    （2）利用上面所得的结论，用不同的割法分别把下面两个三角形面积4等分，（只要割线不同就算一种）精英家教网
    （3）已知：AD为△ABC的中线，点E为AD边上的中点，若△ABC的面积为20，BD=4，求点E到BC边的距离为多少？精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

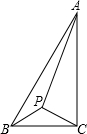    （2013•松北区一模）如图，P为△ABC内一点，∠BAC=30°，∠ACB=90°，∠BPC=120°．若BP=
    		3
    ，则△PAB的面积为
    3
    		3
    2
    3
    		3
    2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

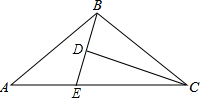    （2013•邯郸一模）如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE．若AC=5，BC=3，则BD的长为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•白云区一模）如图，D为△ABC的AB边上一点，E为AC延长线上的一点，且CE=BD．
    （1）当AB=AC时，求证：DE＞BC；
    （2）当AB≠AC时，DE与BC有何大小关系？给出结论，画出图形，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，P为△ABC的边BC上的任意一点，设BC=a，BC边上的高AH为h．作△ABC的中位线B1C1，连接PB1、PC1；作△AB1C1的中位线B2C2，连接PB2、PC2；…；这样一直作下去，得到一组三角形：△PB1C1、△PB2C2、…、△PBnCn（n为正整数），则△PBnCn的面积为
    2n-1
    22n+1
    ah
    2n-1
    22n+1
    ah
    （用含n、a、h的式子表示）．

    查看答案和解析>>

    同步练习册答案