
 如图,直线AB,CD相交于点O,∠AOC=90°,
如图,直线AB,CD相交于点O,∠AOC=90°,分析 (1)根据已知得出∠AOD=90°,∠EOB<90°,∠AOE>90°,即可得出答案;
(2)代入∠EOB=∠BOC+∠EOC求出即可;代入∠EOD=∠AOE+∠AOD求出即可.
解答 解:(1)∵∠AOC=90°,
∴∠AOC=∠AOD=∠BOD=∠BOC=90°,
∴∠AOD=90°,∠EOB>90°,∠AOE<90°,
即∠AOE<∠AOD<∠BOE.
(2)∵∠EOC=28°,∠AOC=90°,∠AOC+AOD=180°,
∴∠EOB=90°+28°=118°,
∴∠EOD=∠AOE+∠AOD=90°-28°+90°=152°.
点评 本题考查了对顶角和邻补角的应用,主要考查学生的计算能力.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
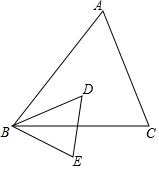 如图,在△ABC和△DBE中,$\frac{AB}{DB}$=$\frac{BC}{BE}$=$\frac{5}{3}$,且∠DBA=∠CBE.
如图,在△ABC和△DBE中,$\frac{AB}{DB}$=$\frac{BC}{BE}$=$\frac{5}{3}$,且∠DBA=∠CBE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
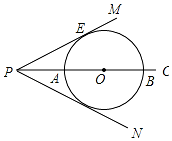 如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
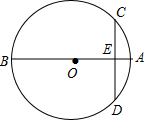 ⊙O的两条弦AB,CD相交于点E.
⊙O的两条弦AB,CD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
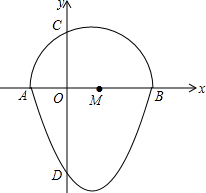 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com