

 =
=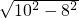 =6,
=6,

 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源:数学:5.4 平行线及平行线的判定 同步练习(人教版七年级下) 人教版 题型:044
已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.

(1)问题的结论:DF________AE.
(2)证明思路分析:欲证DF________AE,只要证∠3=________.
(3)证明过程:
证明:∵CD⊥DA,DA⊥AB,( )
∴∠CDA=∠DAB=________°.(垂直定义)
又∠1=∠2,( )
从而∠CDA-∠1=________-________,(等式的性质)
即∠3=________.
∴DF________AE.(________,________)
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:013
A.平移 B.旋转 C.翻折 D.以上都不对

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com