
直角三角形的两条边长分别是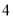 和
和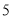 ,则此三角形的面积为__________.
,则此三角形的面积为__________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型:解答题
已知多项式2x2+3xy﹣2y2﹣x+8y﹣6可分解为(x+2y+m)(2x﹣y+n)的形式.试求:m、n的值?
m=-2,n=3. 【解析】试题分析:首先利用多项式乘法去括号,进而得出对应同类项系数相同,进而求出即可. 试题解析:∵(x+2y+m)(2x﹣y+n) =2x2﹣xy+nx+4xy﹣2y2+2yn+2mx﹣my+mn =2x2+3xy﹣2y2+(n+2m)x+(2n﹣m)y﹣6, ∴ ,解得: .查看答案和解析>>
科目:初中数学 来源:山东省聊城市莘县2017-2018学年八年级(上)期末模拟数学试卷(含答案) 题型:单选题
过点(﹣2,﹣4)的直线是( )
A. y=x﹣2 B. y=x+2 C. y=2x+1 D. y=﹣2x+1
A 【解析】把点x=-2代入A中的解析式y=x﹣2,可以得y=-4,故选A.查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级(上)期中数学试卷 题型:单选题
﹣3的倒数是( )
A. 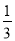 B. -
B. -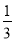 C. ±
C. ±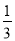 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年八年级上学期期中考试数学试卷(含解析) 题型:解答题
(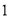 )解不等式:
)解不等式: 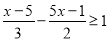 .
.
(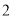 )解不等式组:
)解不等式组: 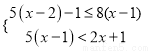 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
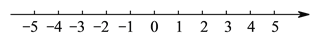
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年八年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,在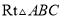 和
和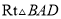 中,
中, 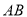 为斜边,
为斜边, 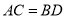 ,
, 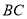 ,
, 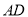 相交于点
相交于点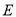 ,下列说法错误的是( ).
,下列说法错误的是( ).
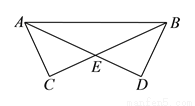
A. 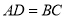 B.
B. 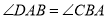 C.
C. 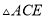 ≌
≌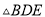 D.
D. 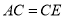
查看答案和解析>>
科目:初中数学 来源:重庆市2017-2018学年七年级(上)期中数学试卷 题型:解答题
某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x 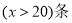 .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若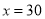 ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当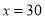 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源:重庆市2017-2018学年七年级(上)期中数学试卷 题型:单选题
下列说法中正确有几个( )
①﹣a是负数 ②|a|一定不是负数 ③|﹣a|一定是负数 ④﹣a2一定是负数.
A. 0 B. 3 C. 2 D. 1
D 【解析】①a为0或负数时不成立,所以错误;②符合绝对值的非负性,所以正确;③a=0时不成立,所以错误;④a=0时不成立,所以错误, 故选D.查看答案和解析>>
科目:初中数学 来源:山东省临沂市沂南县2016-2017上学期八年级期末数学调研试卷 题型:填空题
如图所示,在等边三角形△ABC中,AQ=PQ,PR=PS,PR⊥AB 于R,PS⊥AC于S,下列说法:①点P在∠BAC的平分线上;②AS=AR;③QP∥AR; ④△BRP≌△QSP.其中结论正确的是 _______________.(只填序号)
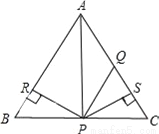
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com