-2
分析:根据一元二次方程ax
2+bx+c=0(a≠)解的定义和根与系数的关系得到x
12-4x
1+m=0,x
22-4x
2+m=0,x
1+x
2=4,x
1•x
2=m,变形为x
12-3x
1+=x
1-m=0,x
22-3x
2=x
2-m,根据题意有(x
1-m)(x
2-m)=10,展开得到x
1•x
2-m(x
1+x
2)+m
2=10,于是m-m×4+m
2=10,解此方程得到m
1=5,m
2=-2,然后把它们分别代入原方程,计算根的判别式来确定m的值.
解答:∵x
1、x
2是关于x方程x
2-4x+m=0的两个实数根,
∴x
12-4x
1+m=0,x
22-4x
2+m=0,x
1+x
2=4,x
1•x
2=m
∴x
12-3x
1+=x
1-m=0,x
22-3x
2=x
2-m,
∴(x
1-m)(x
2-m)=10,
∴x
1•x
2-m(x
1+x
2)+m
2=10,
∵m-m×4+m
2=10,
整理得m
2-3m-10=0,
解得m
1=5,m
2=-2,
当m=5,方程化为x
2-4x+5=0,由于△=16-4×5<0,此方程无实数解;
当m=-2,方程化为x
2-4x-2=0,由于△=16+4×2>0,此方程有两个实数解;
所以m=-2.
故答案为-2.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠)的根与系数的关系:若方程两根分别为x
1,x
2,则x
1+x
2=-

,x
1•x
2=

.也考查了一元二次方程根的判别式及其解的定义.

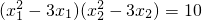 ,则m=________.
,则m=________. ,x1•x2=
,x1•x2= .也考查了一元二次方程根的判别式及其解的定义.
.也考查了一元二次方程根的判别式及其解的定义. 

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案