
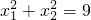 ,则k=________.
,则k=________. 或-2
或-2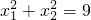 ,得(x1+x2)2-2x1•x2=9,然后把x1+x2=-(k+1),x1•x2=-k2代入得到关于k的一元二次方程3k2+2k-8=0,利用因式分解法解方程即可得到k的值.
,得(x1+x2)2-2x1•x2=9,然后把x1+x2=-(k+1),x1•x2=-k2代入得到关于k的一元二次方程3k2+2k-8=0,利用因式分解法解方程即可得到k的值.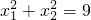 ,
, ,k2=-2,
,k2=-2, 或-2.
或-2. 或-2.
或-2. ,x1•x2=
,x1•x2= .也考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式以及一元二次方程的解法.
.也考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式以及一元二次方程的解法. 

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com