
如图,在平面直角坐标系中,双曲线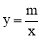 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
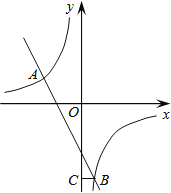
(1)求双曲线和直线的解析式;
(2)直接写出不等式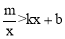 的解集.
的解集.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源:北师大版九年级上学数学第一章检测题 题型:填空题
如图,在正方形ABCD中,点E是对角线BD上任意一点,过点E作EF⊥BC于点F,作EG⊥CD于点G,若正方形ABCD的周长为a,则四边形EFCG的周长为_____.
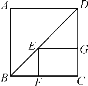
查看答案和解析>>
科目:初中数学 来源:2018-2019学年北师版七年级数学上册专题复习 整式及其加减 题型:解答题
先化简,再求值:-a2b+(3ab2-a2b)-2(2ab2-a2b),其中 a=-1,b=-2.
查看答案和解析>>
科目:初中数学 来源:2018-2019学年北师版七年级数学上册专题复习 整式及其加减 题型:单选题
若|x+y+2|+(xy-1)2=0,则(3x-xy+1)-(xy-3y-2)的值为( )
A. 3 B. -3 C. -5 D. 11
查看答案和解析>>
科目:初中数学 来源:2018-2019学年北师版七年级数学上册专题复习 整式及其加减 题型:单选题
对于式子: ,
, ,
, ,3x2+5x-2,abc,0,
,3x2+5x-2,abc,0, ,m,下列说法正确的是( )
,m,下列说法正确的是( )
A. 有5个单项式,1个多项式 B. 有3个单项式,2个多项式
C. 有4个单项式,2个多项式 D. 有7个整式
查看答案和解析>>
科目:初中数学 来源:北师大版九年级上学数学第六章检测题 题型:填空题
如图,已知点A,C在反比例函数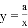 (a> 0)的图象上,点B,D在反比例函数
(a> 0)的图象上,点B,D在反比例函数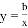 (b <0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB = 3,CD = 2,AB与CD的距离为5,则a -b的值是________.
(b <0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB = 3,CD = 2,AB与CD的距离为5,则a -b的值是________.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级上学数学第六章检测题 题型:单选题
如图,直线y= x与双曲线y=
x与双曲线y= (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y= (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
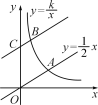
A. 3 B. 6 C.  D.
D. 
查看答案和解析>>
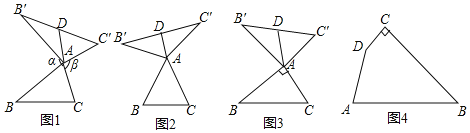
科目:初中数学 来源:内蒙古包头市东河区2018届九年级中考二模试卷数学试卷 题型:解答题
我们定义:如图1,在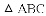
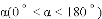 得到
得到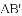
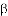
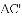
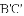
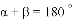 时,我们称
时,我们称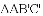
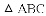
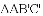
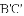
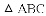
特例感知:
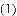
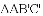
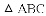
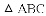

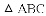
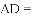
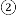
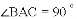 ,
,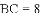
猜想论证:
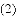
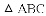
拓展应用
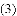
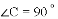 ,
,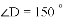 ,
,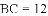
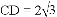 ,
,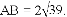 在四边形内部是否存在点P,使
在四边形内部是否存在点P,使
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com