
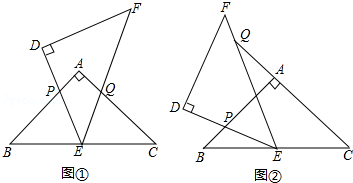
(1)两个全等的等腰直角三角形ABC和三角形EDA如图放置,点B,A,D,在同一条直线上.那么点C,A,E在同一条直线上;

①在上图中,作∠ABC的平分线BF,过点D作DF⊥BF,垂足为F;
②猜想:线段BF,CE的关系,结论是:________.
(2)将(1)中的“等腰直角三角形”换成“直角三角形”,其它条件不变,如图,连结CE,请问你猜想的BF与CE的关系是否仍然成立?若成立,请证明,若不成立,请说明理由.

|
(1)①画图. 1分
②结论是:BF⊥CE,BF= (2)如图. ①证明BF= ∵BF为∠ABF的平分线,∠ABC=90°, ∴∠CBF=∠ABF=45°. ∵DF⊥BF, ∴∠F=90°. ∵点B,A,D在同一条直线上, ∴△BFD为直角三角形. ∴cos∠FBD= ∴BF= 又∵Rt△ABC≌Rt△EDA, ∴BC=AD,BA=DE. 设BC=AD=a,BA=DE=b, ∴BD=a+b. ∴BF= 过E作EH∥BD交CB的延长线于H. ∵∠CBA=90°,∠ADE=90°, ∴∠CBA=∠ADE. ∴CH∥DE. ∴四边形BHED为矩形. ∴BH=DE=b,HE=BD=a+b. ∴CH=a+b. ∴△HCE等腰直角三角形. 由勾股定理,得CE= ∴BF= ②证明BF⊥CE. ∵Rt△CHE是等腰直角三角形, ∴∠HCE=∠HEC=45°. ∵∠FBC=45°, ∴∠BGE=∠HCE+∠FBC=90° ∴BF⊥CE. 7分 ∴BF⊥CE,BF= |


科目:初中数学 来源: 题型:
 10、如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别与AD、AE相交于点F、G.图中共有n对三角形相似(相似比不等于1),则n的值是( )
10、如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别与AD、AE相交于点F、G.图中共有n对三角形相似(相似比不等于1),则n的值是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
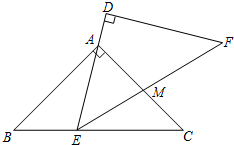 如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com