
已知x1,x2是关于x的一元二次方程x2﹣6x+k=0的两个实数根,且x12x22﹣x1﹣x2=115.
(1)求k的值;
(2)求x12+x22+8的值.
(1)k的值为﹣11;(2)x12+x22+8=66. 【解析】试题分析:(1)方程有两个实数根,必须满足△=b2-4ac≥0,从而求出实数k的取值范围,再利用根与系数的关系,x12x22-x1-x2=115.即x12x22-(x1+x2)=115,即可得到关于k的方程,求出k的值. (2)根据(1)即可求得x1+x2与x1x2的值,而x12+x22+8=(x1+x2)2-2x1x2+... 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:填空题
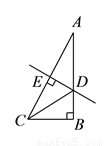
如图,在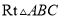 中,
中, 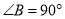 ,
, 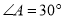 ,
, 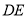 垂直平分斜边
垂直平分斜边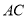 ,交
,交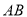 于
于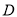 ,
, 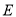 是垂足,连接
是垂足,连接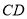 ,若
,若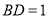 ,则
,则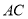 的长是__________.
的长是__________.
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:单选题
下列图案中,是轴对称图形但不是中心对称图形的有( )

A.1个 B.2个 C.3个 D.4个
A. 【解析】 试题分析:根据轴对称图形与中心对称图形的概念可得第一个图形,是轴对称图形但也是中心对称图形;第二个图形,是轴对称图形,不是中心对称图形;第三个图形,不是轴对称图形,是中心对称图形;第四个图形,是轴对称图形,也是中心对称图形.所以只有第二个图形是轴对称图形但不是中心对称图形.故选A.查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
如果鸭绿江水位高1m时水位变化记作+1m,那么水位下降0.5m时水位变化记作( )
A. ﹣0.5m B. 0.5m C. 1.5m D. ﹣1.5m
A 【解析】∵水位升高1m时水位变化记作+1m, ∴水位下降0.5 m时水位变化记作﹣0.5m, 故选A.查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
下列计算中,正确的是( )
A. ﹣2(a+b)=﹣2a+b B. ﹣2(a+b)=﹣2a﹣b2
C. ﹣2(a+b)=﹣2a﹣2b D. ﹣2(a+b)=﹣2a+2b
C 【解析】A、﹣2(a+b)=﹣2a﹣2b,故错误;B、﹣2(a+b)=﹣2a﹣2b,故错误;C、﹣2(a+b)=﹣2a﹣2b,正确;D、﹣2(a+b)=﹣2a﹣2b,故错误, 故选C.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:填空题
如图,△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为_____.

查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:单选题
如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )
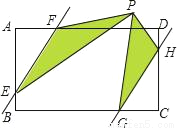
A. 7 B. 8 C. 12 D. 14
A 【解析】连接EG,FH, ∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1, ∴AE=AB?BE=4?1=3, CH=CD?DH=4?1=3, ∴AE=CH, 在△AEF与△CGH中, , ∴△AEF≌△CGH(SAS), ∴EF=GH, 同理可得,△BGE≌△DFH, ∴EG=FH, ∴四边形EGH...查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:填空题
如图,在直角坐标系中,直线y=6﹣x与双曲线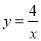 (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
(x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
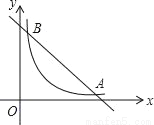
查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
如图,在四边形ABCD中,∠BAD=∠B=∠C=90 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
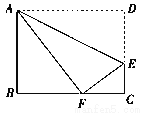
(1)求BF的长;
(2)求CE的长.
(1);(2) 【解析】试题分析:由折叠的性质可得:AF=AD=20,再由勾股定理可求出BF=12. (2)设CE=x,DE=EF=16-x,然后利用勾股定理得到,再解方程求出x即可. (1)∵△AFE是△ADE折叠得到的, ∴. 在Rt△ABE中, (2)∵△AFE是△ADE折叠得到的, ∴. 设,则 在Rt△EFC中, 即 解得...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com