练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图⊙A中，弦CD＝EF．请你至少找出图中4对具有相等关系的量，并就其中的一对说明理由(半径相等除外)．

    答案：
    解析：

    　　解：每写出一对给2分，共8分，多写不加分；对其中一对说明理由正确给2分．相等关系的量如：∠C＝∠D，∠E＝∠F，∠CAD＝∠EAF，∠EAD＝∠CAF，……


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2008年浙江省台州市初中毕业升学统一考试、数学试卷及答案 题型：022

    善于归纳和总结的小明发现，“数形结合”是初中数学的基本思想方法，被广泛地应用在数学学习和解决问题中．用数量关系描述图形性质和用图形描述数量关系，往往会有新的发现．小明在研究垂直于直径的弦的性质过程中(如图，直径AB⊥弦CD于E)，设AE＝x，BE＝y，他用含x，y的式子表示图中的弦CD的长度，通过比较运动的弦CD和与之垂直的直径AB的大小关系，发现了一个关于正数x，y的不等式，你也能发现这个不等式吗？写出你发现的不等式________．

    查看答案和解析>>

    科目：初中数学 来源：江西省2012年初中毕业暨中等学校招生考试数学试题 题型：044

    已知，纸片⊙O的半径为2，如图1，沿弦AB折叠操作．

    (1)如图2，当折叠后的AB经过圆心O时，求AB弧的长；

    (2)如图3，当弦AB＝2时，求折叠后AB弧所在圆的圆心O′到弦AB的距离；

    (3)在图1中，再将纸片⊙O沿弦CD折叠操作．

    ①如图4，当AB∥CD，折叠后的CD弧与AB弧所在圆外切于点P，设点O到弦AB、CD的距离之和为d，求d的值；

    ②如图5，当AB与CD不平行，折叠后的CD弧与AB弧所在圆外切于点P时，设点M为AB的中点，点N为CD的中点．试探究四边形OMPN的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：江西省南昌市2012年中考数学试题 题型：044

    已知，纸片⊙O的半径为2，如图1，沿弦AB折叠操作．

    (1)①折叠后的所在圆的圆心为时，求的长度；

    ②如图2，当折叠后的经过圆心为O时，求的长度；

    ③如图3，当弦AB＝2时，求圆心O到弦AB的距离；

    (2)在图1中，再将纸片⊙O沿弦CD折叠操作．

    ①如图4，当AB∥CD，折叠后的与所在圆外切于点P时，设点O到弦AB．CD的距离之和为d，求d的值；

    ②如图5，当AB与CD不平行，折叠后的与所在圆外切于点P时，设点M为AB的中点，点N为CD的中点，试探究四边形OMPN的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：中考真题 题型：解答题

    已知，纸片⊙Ｏ的半径为2 ，如图1. 沿着弦AB 折叠操作。
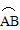    （1）如图2 ，当折叠后的经过圆心Ｏ时，求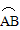的长度；
    （2）如图3，当弦AB＝2时，求折叠后⊙O所在圆的圆心O′到弦AB的距离；
    （3）在如图1中，将纸片⊙O沿着弦CD折叠操作：    
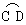    ①如图4，当AB∥CE时，折叠后的和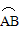所在圆外切与点P时，设点O到弦CD，AB的距离之和为d，试求d的值；  
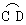    ②如图5，当AB与CD不平行时，折叠后的和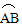所在圆外切与点P，点M，N分别为AB，CD的中点试探究四边形OMPN的形状，并证明。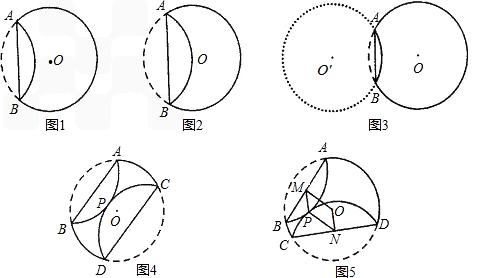

    查看答案和解析>>

    同步练习册答案