如图，数轴上的六个点满足AB=BC=CD=DE=EF，则在点B、C、D、E对应的数中，最接近﹣10的点是（ ）
A. 点B B. 点C C. 点D D. 点E
科目：初中数学 来源：2018年6月内蒙古兴安盟中考数学模拟试卷 题型：解答题
直角坐标系中，已知A（1，0），以点A为圆心画圆，点M（4，4）在⊙A上，直线y=﹣
x+b过点M，分别交x轴、y轴于B、C两点．
（1）①填空：⊙A的半径为 ，b= ．（不需写解答过程）
②判断直线BC与⊙A的位置关系，并说明理由．
（2）若EF切⊙A于点F分别交AB和BC于G、E，且FE⊥BC，求
的值．
（3）若点P在⊙A上，点Q是y轴上一点且在点C下方，当△PQM为等腰直角三角形时，直接写出点Q的坐标．
查看答案和解析>>
科目：初中数学 来源：2018年广东省东莞市堂镇六校考数学模拟试卷 题型：填空题
已知A（a﹣5，2b﹣1）在y轴上，B（3a+2，b+3）在x轴上，则C（a，b）向左平移2个单位长度再向上平移3个单位长度后的坐标为_____．
查看答案和解析>>
科目：初中数学 来源：2018年广东省东莞市堂镇六校考数学模拟试卷 题型：单选题
关于x的方程|x2﹣x|﹣a=0，给出下列四个结论：
①存在实数a，使得方程恰有2个不同的实根； ②存在实数a，使得方程恰有3个不同的实根；
③存在实数a，使得方程恰有4个不同的实根；④存在实数a，使得方程恰有6个不同的实根；
其中正确的结论个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源：江苏省镇江市润州区2018届九年级中考模拟试卷数学试卷 题型：解答题
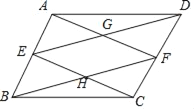
如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，AF与DE相交于点G，BF与CE相交于点H．
（1）求证：四边形EHFG是平行四边形；
（2）①若四边形EHFG是菱形，则平行四边形ABCD必须满足条件 ；
②若四边形EHFG是矩形，则平行四边形ABCD必须满足条件 ．
查看答案和解析>>
科目：初中数学 来源：2018年湖南省长沙市中考数学模拟试卷（3月份） 题型：解答题
设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．如函数y=﹣x+4，当x=1时，y=3；当x=3时，y=1，即当1≤x≤3时，恒有1≤y≤3，所以说函数y=﹣x+4是闭区间[1，3]上的“闭函数”，同理函数y=x也是闭区间[1，3]上的“闭函数”．
（1）反比例函数y=
是闭区间[1，2018]上的“闭函数”吗？请判断并说明理由；
（2）如果已知二次函数y=x2﹣4x+k是闭区间[2，t]上的“闭函数”，求k和t的值；
（3）如果（2）所述的二次函数的图象交y轴于C点，A为此二次函数图象的顶点，B为直线x=1上的一点，当△ABC为直角三角形时，写出点B的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B. 
C. 
D. 
的值．
，如3?2=
=
，那么8?5=_____．