解:(1)⊙O与BC相交.理由如下:
如图1,过点E作EF⊥BC于点F.
∵DE是△ABC的中位线,
∴DE∥BC,DE=

BC=5,BE=

AB=3,
∴⊙O的半径为

,DE与BC间的距离就是EF的长度.
∵sin∠B=
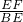
=

,即
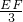
=

,
∴EF=

.
∵

>

,
∴⊙O与BC相交;
(2)①设⊙O半径为r
1.
∵⊙O与BC相切,
∴OF⊥BC.
∵Rt△COF∽Rt△CBA,
∴

=
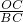
,即

=

,
∴r
1=3,即⊙O半径为3;
②设⊙O半径为r
2.
∵BC与⊙O相切,
∴OF⊥BC.
过点A作AH⊥BC交DE于G,交BC于点H.则GH=OF=r
2.
∵

AB•AC=

BC•AH,即6×8=10×AH,
∴AH=

.
∵DE∥BC,
∴△AED∽△ABC,
∴

=

,即

=

,
∴

=

,
解得.r
2=
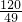
,即⊙O半径为
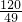
;
③连接OA.要使得⊙O半径最小,则要OA+OF最小,此时,A,O,F三点共线且A,O,F所在直线垂直于BC.
即AO+OF=

,
即⊙O半径最小为:

(AO+OF)=

.

分析:(1)如图1,过点E作EF⊥BC于点F.利用两平行线间的距离的定义知EF即DE与BC间的距离,由三角形中位线定理求得⊙O的半径,然后通过比较EF与⊙O的半径的大小关系即可确定直线与圆的位置关系;
(2)①设⊙O半径为r
1.根据相似三角形Rt△COF∽Rt△CBA的对应边成比例列出比例式

=
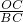
,即

=

,易求r
1=3;
②作直角三角形ABC斜边上的高线AH.利用相似三角形△AED∽△ABC的对应高线之比等于相似比的性质列出比例式

=

,即

=

,易求r
2=
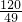
;
③当AF⊥BC,即A、O、F三点共线时,⊙O的半径最小.
点评:本题考查了圆的综合题.注意:勾股定理的逆定理、直角三角形的面积、解直角三角形、切线的性质以及“相似三角形的对应边成比例,相似三角形的对应边上高线之比等于相似比”等相似三角形的性质,在本题的解答过程中的综合运用.


 BC=5,BE=
BC=5,BE= AB=3,
AB=3, ,DE与BC间的距离就是EF的长度.
,DE与BC间的距离就是EF的长度.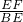 =
= ,即
,即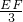 =
= ,
, .
. >
> ,
, =
=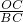 ,即
,即 =
= ,
, AB•AC=
AB•AC= BC•AH,即6×8=10×AH,
BC•AH,即6×8=10×AH, .
. =
= ,即
,即 =
= ,
, =
= ,
,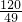 ,即⊙O半径为
,即⊙O半径为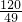 ;
; ,
, (AO+OF)=
(AO+OF)= .
.
 =
=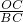 ,即
,即 =
= ,易求r1=3;
,易求r1=3; =
= ,即
,即 =
= ,易求r2=
,易求r2=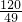 ;
;

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为