练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，AD⊥BC于D，∠B＝2∠C

    求证：AB＋BD＝DC

    答案：
    解析：

    　　解析：证明线段的和差问题，可考虑延长加倍，或在长线段上截取短线段等方法，根据已知条件AD⊥BC，所以可以考虑利用线段垂直平分线的性质定理，在DC上截取DE＝BD，连AE，∵AD⊥BC，DE＝BD

    　　∴AD是BE的垂直平分线，又∵点A在AD上，

    　　∴AB＝AE，∠1＝∠B，

    　　∴∠1＝∠2＋∠C　∠B＝2∠C　∠2＝∠C

    　　∴AE＝EC　∵CE＋DE＝DC　∴AB＋BD＝DC

    　　点评：构造线段垂直平分线把分散的条件相对集中，实现了问题的转化，从而使隐蔽的问题明显化，希望同学们要学会这种转化方法．本题涉及的知识点有：①线段垂直平分线性质定理②三角形的外角等于和它不相邻的两内角的和③等量代换、等式性质等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    15、如图，AD⊥BC于D，DE∥AC，则∠C与∠ADE之和为
    90
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

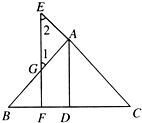    23、已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．
    求证：AD平分∠BAC，填写分析和证明中的空白．
    分析：要证明AD平分∠BAC，只要证明
    ∠BAD
    =
    ∠CAD
    ，
    而已知∠1=∠2，所以应联想这两个角分别和∠1、∠2的关系，由已知BC的两条垂线可推出
    EF
    ∥
    AD
    ，这时再观察这两对角的关系已不难得到结论．
    证明：∵AD⊥BC，EF⊥BC（已知）
    ∴
    EF
    ∥
    AD
    （
    在同一平面内，垂直与同一直线的两直线平行
    ）
    ∴
    ∠1
    =
    ∠BAD
    （两直线平行，内错角相等），
    ∠2
    =
    ∠CAD
    （两直线平行，同位角相等）
    ∵
    ∠1=∠2
    （已知）
    ∴
    ∠BAD=∠CAD
    ，即AD平分∠BAC（
    角平分线的定义
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    22、如图，AD⊥BC于D，EF⊥BC于F，且∠E=∠1，求证∠BAD=∠CAD．
    证明：∵AD⊥BC，EF⊥BC，
    ∴∠EFD=∠ADC=90°（垂线的定义）
    ∴
    EF
    ∥
    AD
    （同位角相等，两直线平行）
    ∴∠BAD=∠1（
    两直线平行，内错角相等
    ），
    ∠CAD=∠E（
    两直线平行，同位角相等
    ）
    又∵∠E=∠1（已知）
    ∴∠BAD=∠CAD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、如图，AD⊥BC于D，EF⊥BC于E，∠1=∠2，AB与DG平行吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•义乌市）如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连结OC，若∠AOC=125°，则∠ABC=
    70°
    70°
    ．

    查看答案和解析>>

    同步练习册答案