(1)证明:∵B(-3,0),C(3,0),
∴OB=OC,
∴y轴是BC的垂直平分线,
又∵点A在y轴正半轴上,点P在线段OA上,
∴AB=AC,PB=PC,
∴∠ABC=∠ACB,∠PBC=∠PCB,
在△BCF和△CBE中,

,

∴△BCF≌△CBE(ASA),
∴BE=CF;
(2)解:如图,连接OF,
∵m=4,OB=3,
∴S
△AOB=

×3×4=6,
∵BF=2AF,
∴S
△BOF=
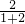
×6=4,S
△AOF=

×6=2,
∴

y
F•3=4,

(-x
F)•4=2,
解得y
F=

,x
F=-1,
∴点F的坐标为(-1,

);
(3)解:设∠BAC=α,
∵S
△BCG=S
△BCA,△BCG和△BCA都是等腰三角形,BC是公共边,
∴BE=BA,
∴∠BEA=∠BAE=α,
∴∠ACB=90°-∠OAC=90°-

α,
在△ABE中,∠BEA+∠BAE=2α<180°,
∴α<90°,
在△BEC中,∠AEB>∠ACB,
∴α>90°-

α,
解得α>60°,
故60°<α<90°,
当α=60°时,△ABC是等边三角形,
∵OC=3,
∴m=AO=

OC=3

,
当α=90°时,△ABC是等腰直角三角形,
m=AO=OC=3,
∴m的取值范围是3<m<3

.
分析:(1)根据点B、C的坐标判断出y轴是BC的垂直平分线,再根据线段垂直平分线上的点到线段两端点的距离相等可得AB=AC,PB=PC,根据等边对等角可得∠ABC=∠ACB,∠PBC=∠PCB,然后利用“角边角”证明△BCF和△CBE全等,根据全等三角形对应边相等可得BE=CF;
(2)连接OF,先求出△AOB的面积,再根据等高的三角形的面积的比等于底边的比求出△BOF和△AOF的面积,再根据三角形的面积列式求出点F的横坐标与纵坐标的长度,从而得解;
(3)设∠BAC=α,根据三角形的面积求出BE=BA,根据等边对等角可得∠BEA=∠BAE=α,根据等腰三角形三线合一的性质和直角三角形两锐角互余求出∠ACB,再根据三角形的内角和定理求出α<90°,根据三角形的一个外角大于任何一个与它不相邻的内角可得∠AEB>∠ACB,然后求出α>60°,然后分α=60°和90°时求出m的值即可得解.
点评:本题考查了全等三角形的判定与性质,三角形的面积,坐标与图形性质,等腰三角形的判定与性质,(2)从三角形的面积考虑求出点F的横坐标与纵坐标是解题的关键,(3)根据三角形的面积求出BE=BA并求出∠BAC的范围是解题的关键,也是本题的难点.

 如图,平面直角坐标系中,已知B(-3,0),C(3,0),点A(0,m)在y
如图,平面直角坐标系中,已知B(-3,0),C(3,0),点A(0,m)在y ,
,
 ×3×4=6,
×3×4=6,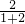 ×6=4,S△AOF=
×6=4,S△AOF= ×6=2,
×6=2, yF•3=4,
yF•3=4, (-xF)•4=2,
(-xF)•4=2, ,xF=-1,
,xF=-1, );
); α,
α, α,
α, OC=3
OC=3 ,
, .
.

 阅读快车系列答案
阅读快车系列答案 =2
=2
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.