
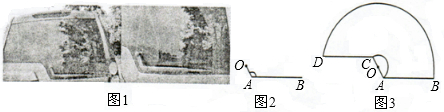
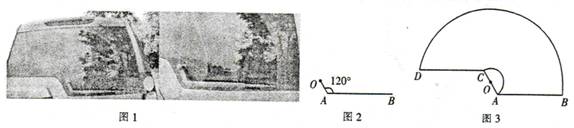
如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB.如图2所示,量杆OA长为10 cm,雨刮杆AB长为48 cm,∠OAB=120°.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.

(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留![]() 的整数倍)
的整数倍)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,可使用科学计算器)
,可使用科学计算器)
科目:初中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 721 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.
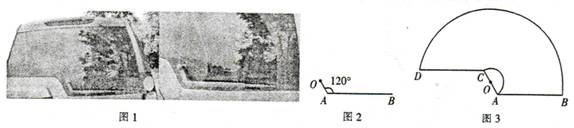
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°=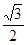 ,cos60°=
,cos60°=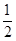 ,tan60°=
,tan60°=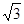 ,
,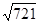 ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:解答题
如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°= ,cos60°=
,cos60°=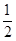 ,tan60°=
,tan60°=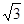 ,
,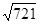 ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,cos60°=
,cos60°= ,tan60°=
,tan60°= ,
,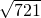 ≈26.851,可使用科学记算器)
≈26.851,可使用科学记算器)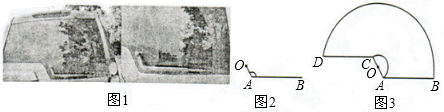
查看答案和解析>>
科目:初中数学 来源:2013年江西省南昌市中考数学试卷(解析版) 题型:解答题
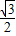 ,cos60°=
,cos60°= ,tan60°=
,tan60°=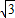 ,
,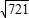 ≈26.851,可使用科学记算器)
≈26.851,可使用科学记算器)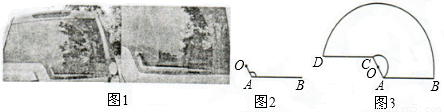
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com