练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

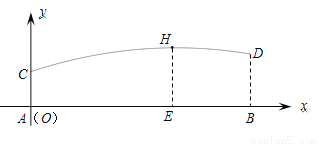
    甲、乙两人分别站在相距6米的A、B两点练习打羽毛球，已知羽毛球飞行的路线为抛物线的一部分，甲在离地面1米的C处发出一球，乙在离地面1.5米的D处成功击球，球飞行过程中的最高点H与甲的水平距离AE为4米，现以A为原点，直线AB为x轴，建立平面直角坐标系（如图所示）．求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度．

    ， ． 【解析】试题分析：根据待定系数法求出抛物线的表达式，求出最大值即可. 试题解析：由题意得：C（0，1），D（6，1.5），抛物线的对称轴为直线 设抛物线的表达式为 则据题意得： ． 解得： ， ∴羽毛球飞行的路线所在的抛物线的表达式为 ． ∵ ，∴飞行的最高高度为米．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年陕西省西安市中考数学模拟试卷 题型：解答题

    化简 ．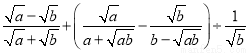

    【解析】试题分析：括号内先进行约分运算，然后通分进行加减运算后进行乘法运算，最后与前面的式子通分进行加减运算即可得. 试题解析：原式= = = = .

    查看答案和解析>>

    科目：初中数学 来源：2017学年第一学期上海（闵行区）九年级数学质量调研试卷 题型：单选题

    下列线段中，能成比例的是（　　）

    A. 3cm、6cm、8cm、9cm B. 3cm、5cm、6cm、9cm

    C. 3cm、6cm、7cm、9cm D. 3cm、6cm、9cm、18cm

    D 【解析】如果两条线段的乘积等于另外两条线段的乘积，则这四条线段叫作成比例线段.因此所给选项中，只有D符合，3×18=6×9，故选D.

    查看答案和解析>>

    科目：初中数学 来源：陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    点P1（x1，y1），点P2（x2，y2）是一次函数y=-4x+3图象上的两个点，且x1＜x2，则y1与y2的大小关系是（　　）

    A. y1＞y2 B. y1＞y2＞0 C. y1＜y2 D. y1=y2

    A 【解析】试题分析：根据一次函数y=kx+b（k≠0，k，b为常数），当k＜0时，y随x的增大而减小解答即可． 【解析】 根据题意，k=﹣4＜0，y随x的增大而减小， 因为x1＜x2，所以y1＞y2． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：陕西省宝鸡市2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    已知直角三角形两边的长为3和4，则此三角形的周长为（　　）

    A. 12 B. 7+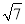 C. 12或7+ 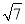D. 以上都不对

    C 【解析】设Rt△ABC的第三边长为x， ①当4为直角三角形的直角边时，x为斜边， 由勾股定理得，x=5，此时这个三角形的周长=3+4+5=12； ②当4为直角三角形的斜边时，x为直角边， 由勾股定理得,x=,此时这个三角形的周长=3+4+=7+ 综上所述,此三角形的周长为12或7+. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017学年度第一学期上海（杨浦区）期末考试初三数学试卷 题型：填空题

    已知抛物线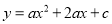，那么点P（-3，4）关于该抛物线的对称轴对称的点的坐标是______．

    （1，4）. 【解析】试题解析：抛物线的对称轴为： 点关于该抛物线的对称轴对称的点的坐标是 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017学年度第一学期上海（杨浦区）期末考试初三数学试卷 题型：填空题

    点A（-1，m）和点B（-2，n）都在抛物线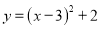上，则m与n的大小关系为m______n（填“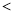”或“”）．

    ＜. 【解析】试题解析：当时， 当时， 故答案为：

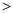    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市宁城县2018届九年级上学期期末数学试卷 题型：解答题

    某新建小区要在一块等边三角形内修建一个圆形花坛.

    （1）要使花坛面积最大，请你用尺规画出圆形花坛示意图；（保留作图痕迹，不写做法）

    （2）若这个等边三角形的周长为36米，请计算出花坛的面积.

    （1）见解析；（2）12π米2. 【解析】试题分析：（1）分别作出三角形任意两角的角平分线，交点即是圆心，再以到任意一边的距离为半径画圆即可得出答案； （2）利用等边三角形的性质，任意边上的三线合一，即可得出∠OBD=30°，BD=6，再利用tan∠OBD=求出即可，再利用圆的面积公式求出． 试题解析：（1）用尺规作三角形的内切圆如图， （2）∵等边三角形的周长为36米， ∴...

    查看答案和解析>>

    科目：初中数学 来源：贵州省贵阳市2017-2018学年七年级（上）期末模拟数学试卷 题型：解答题

    若式子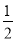a的值比式子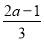的值大1．

    （1）求a的值；

    （2）求关于x的方程a（x﹣4）=x+1的解．

    （1）a=﹣4；（2）x=3． 【解析】试题分析：（1）根据题意列出方程，解方程即可得； （2）把（1）中计算出的a的值代入可得：﹣4（x﹣4）=x+1，再解方程即可得. 试题解析：（1）【解析】 由题意可知： ，解得：a=﹣4； （2）将a=﹣4代入方程a（x﹣4）=x+1得：﹣4（x﹣4）=x+1，解得：x=3．

    查看答案和解析>>

    同步练习册答案