Question

3．已知A（3，2），点B是x轴上的动点，设B（t，0），过A作AB的垂线交y轴与C，点D是BC的中点．
（1）当点D在x轴上时，求B点坐标及直线AC的解析式．
（2）如图1．当点D在第一象限时，若直线OD与过点D的双曲线的另一支交于点F．将点B关于y轴作轴对称变换得点B′，连接DB′．FB′．FB．
①求证：四边形DB′FB为平行四边形．
②当t为何值时，四边形DB′FB为矩形．
（3）如图2，设过点D画y轴的垂线与直线AC交与点E，是否存在点B，使△CDE成为等腰三角形？若存在，请求出点B的坐标；若不存在，请说明理由．

Answer 1

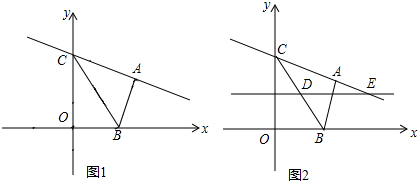
分析 （1）当点D在x轴上时，点C与O重合；作AM⊥x轴于M，根据射影定理求出BM，得出OB，即可求出点B坐标；用待定系数法求出直线AC的解析式；
（2）①根据题意得出OB=OB′，OD=OF，容易证出结论；
②四边形DB′FB为矩形时，OB=OD；先证明△OBD是等边三角形，再用待定系数法求出直线AB和AC的解析式（用含t的式子表示），由两条直线的垂直关系，求出t的值；
（3）分两种情况讨论：①当A、E重合时，CD=BD=x，根据勾股定理求出x，进一步求出OB，得出B的坐标；
②作AM⊥y轴于M，作AN⊥x轴于N；如图4所示，通过两次证明三角形相似求出BO，得出点B的坐标．

解答 解：（1）当点D在x轴上时，点C与O重合；作AM⊥x轴于M，如图1所示：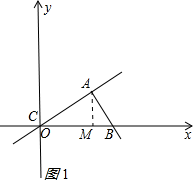
则AM=2，OM=3；
∵AC⊥AB，
根据射影定理得：AM²=OM•BM，
∴BM=$\frac{A{M}^{2}}{OM}$=$\frac{{2}^{2}}{3}$=$\frac{4}{3}$，
∴OB=3+$\frac{4}{3}$=$\frac{13}{3}$，
∴B（$\frac{13}{3}$，0）；
设直线AC的解析式为y=kx，
把点A（3，2）代入得：k=$\frac{2}{3}$，
∴直线AC的解析式为y=$\frac{2}{3}$x；

（2）①如图2所示：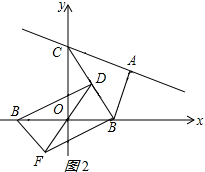
根据题意得：OB=OB′，OD=OF，
∴四边形DB′FB为平行四边形；
②四边形DB′FB为矩形时，OB=OD；
∵∠COB=90°，点D是BC的中点，
∴OD=$\frac{1}{2}$BC=BD，
∴OD=OB=BD，
∴∠OBC=60°，
∴OC=$\sqrt{3}$OB=$\sqrt{3}$t，
∴C（0，$\sqrt{3}$t），
设直线AB的解析式为y=kx+b，
把点A（3，2），B（t，0）代入得：
$\left\{\begin{array}{l}{3k+b=2}\\{kt+b=0}\end{array}\right.$，解得：k=$\frac{2}{3-t}$；
设直线AC的解析式为y=ax+c，
把点A（3，2），C（$\sqrt{3}$t，0）代入得：
$\left\{\begin{array}{l}{3a+c=2}\\{c=\sqrt{3}t}\end{array}\right.$，解得：a=$\frac{2-\sqrt{3}t}{3}$，
∵AC⊥AB，
∴ka=-1，
∴$\frac{2}{3-t}$•$\frac{2-\sqrt{3}t}{3}$=-1，
解得：t=$\frac{26\sqrt{3}}{3}$-13，
∴当t=$\frac{26\sqrt{3}}{3}$-13时，四边形DB′FB为矩形；

（3）①当A、E重合时，如图3所示：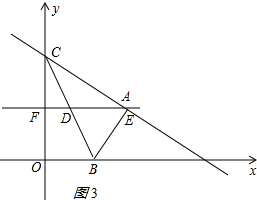
设CD=BD=x，则DE=x，DF=3-x，
∴OB=6-2x，
在Rt△OBC中，OC=4，OC²+OB²=BC²，
即4²+（6-2x）²=（2x）²，
解得：x=$\frac{13}{6}$；
∴OB=6-2×$\frac{13}{6}$=$\frac{5}{3}$，
∴B（$\frac{5}{3}$，0）；
②如图4所示：
作AM⊥y轴于M，作AN⊥x轴于N；
则∠AMC=∠ANB=90°，
∴∠1+∠CAN=90°，∠2+∠CAN=90°，
∴∠1=∠2，
∴△AMC∽△ANB，
∴$\frac{AC}{AB}=\frac{AM}{AN}$=$\frac{3}{2}$，
设AC=3k，AB=2k，则BC=$\sqrt{13}$k，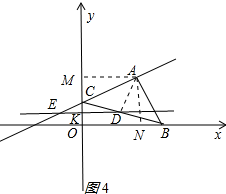
∵△CED是等腰三角形，
∴CE=CD=DB=$\frac{\sqrt{13}}{2}$k，
∵AM∥DE，
∴△AMC∽△EKC，
∴$\frac{EC}{AC}=\frac{EK}{AM}=\frac{\sqrt{13}}{4}$，
∴EK=$\frac{3\sqrt{13}}{4}$，
∴BO=2KD=2EK=$\frac{3\sqrt{13}}{2}$，
∴B（$\frac{3\sqrt{13}}{2}$，0）；
综上所述：点B坐标为（$\frac{5}{3}$，0）或（$\frac{3\sqrt{13}}{2}$，0）．

点评 本题是反比例函数综合题，考查了一次函数解析式的求法、点的坐标、平行四边形的判定、矩形的性质、勾股定理的运用以及相似三角形的判定与性质；本题难度较大，综合性强，有利于培养学生综合运用知识进行推理和计算的能力以及探究精神．