
下列运算中,正确的是( )
A. 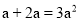 B.
B. 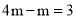 C.
C. 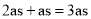 D.
D. 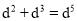
科目:初中数学 来源:内蒙古2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
解方程: 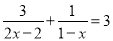
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
下列运算正确的是( ).
A. 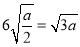 B.
B. 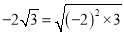
C. 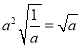 D.
D. 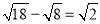
查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年七年级上学期期末联考数学试卷 题型:填空题
若x,y互为相反数,a、b互为倒数,则 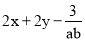 代数式的值为________.
代数式的值为________.
查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年七年级上学期期末联考数学试卷 题型:单选题
下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. 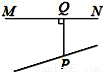 B.
B. 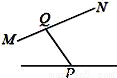 C.
C. 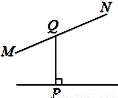 D.
D. 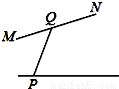
查看答案和解析>>
科目:初中数学 来源:2017-2018学年西藏拉萨市九年级(上)第一次月考数学试卷 题型:解答题
某超市按每件30元的价格购进某种商品,在销售的过程中发现,该种商品每天的销售量w(件)与销售单价x(元)之间满足关系w=﹣3x+150(30≤x≤50),如果销售这种商品每天的利润为y(元),那么销售单价定为多少元时,每天的利润最大?最大利润是多少元?
销售单价定为30元时,每天的利润最大,最大利润是1800元. 【解析】分析:根据题意可以求得y关于x的函数关系式,然后化为顶点式即可解答本题,注意x的取值范围. 本题解析: 由题意可得, y=x(﹣3x+150)=﹣3(x﹣25)2+1875, ∵30≤x≤50, ∴x=30时,y取得最大值,此时y=1800, 即销售单价定为30元时,每天的利润最大,最大...查看答案和解析>>
科目:初中数学 来源:2017-2018学年西藏拉萨市九年级(上)第一次月考数学试卷 题型:填空题
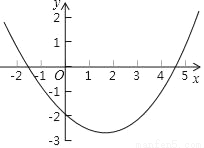
二次函数y=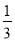 x2﹣x﹣2的图象如图所示,那么关于x的方程
x2﹣x﹣2的图象如图所示,那么关于x的方程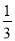 x2﹣x﹣2=0的近似解为_____(精确到0.1).
x2﹣x﹣2=0的近似解为_____(精确到0.1).
查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年八年级数学上册12月联考试卷 题型:解答题
(1) 已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的外角平分线,交CB边的延长线于点D.
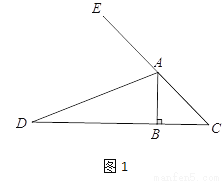
求证:BD=AB+AC.
(2)对于任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图2,请你写出线段AC、AB、BD之间的数量关系并加以证明.
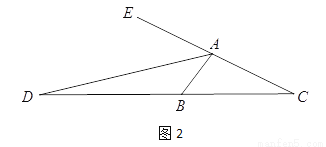
查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2017-2018学年七年级上学期期末联考数学试卷 题型:单选题
如图过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A. 两点确定一条直线 B. 两点之间线段最短
C. 垂线段最短 D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
A 【解析】试题分析:根据:两点确定一条直线,即可解答. 【解析】 经过刨平的木板上的两个点,能弹出一条笔直的墨线此操作的依据是两点确定一条直线. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com