
科目: 来源:2011年连江文笔中学八年级第一学期期中考试数学卷 题型:解答题
如图,四边形ABCD中,AD∥BC,∠ABD=30o,
AB=AD,DC⊥BC于点C,若BD=2,求CD的长.

查看答案和解析>>
科目: 来源:2011年连江文笔中学八年级第一学期期中考试数学卷 题型:解答题
我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线OB长为半径画弧交x 轴于点“A”,请根据图形回答下列问题:

1.线段OA的长度是___________
2.这种研究和解决问题的方式,体现了 的数学思想方法。(将下列符合的选项序号填在横线上)
A. 数形结合 B. 归纳 C. 换元 D. 消元
查看答案和解析>>
科目: 来源:2011年连江文笔中学八年级第一学期期中考试数学卷 题型:解答题
阅读下面的文字,解答问题:
大家都知道 是无理数,而且
是无理数,而且 ,即
,即 ,无理数是无限不循环小数,因此
,无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 来表示
来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:①∵ ,即
,即 ,
,
∴ 的整数部分为1,小数部分为
的整数部分为1,小数部分为 .
.
②∵ ,即
,即 ,[来源:]
,[来源:]
∴ 的整数部分为2,小数部分为
的整数部分为2,小数部分为 .
.
请解答:1. 的整数部分为 ,小数部分为 。
的整数部分为 ,小数部分为 。
2.如果 的小数部分为a,
的小数部分为a, 的整数部分为b,求
的整数部分为b,求 的值;(要求写出解题过程)[来源:ZXXK]
的值;(要求写出解题过程)[来源:ZXXK]
查看答案和解析>>
科目: 来源:2011年连江文笔中学八年级第一学期期中考试数学卷 题型:解答题
已知:点O到△ABC的两边AB、AC所在直线的距离相等,
即OF⊥AB,OE⊥AC ,OF=OE,且OB=OC。
1.如图1,若点O在BC上,求证:AB=AC;
2.如图2,若点O在△ABC的内部,求证:AB=AC;
3.若点O在△ABC外部,猜想:AB=AC还成立吗?请画图,并加以证明。

查看答案和解析>>
科目: 来源:2011年重庆名校中考数学函数综合试题精练 题型:选择题
如图,已知抛物线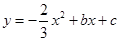 与
与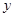 轴交于点
轴交于点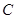 ,与
,与 轴交与A、B两点(点A在点B的左侧),且OA=1,OC=2
轴交与A、B两点(点A在点B的左侧),且OA=1,OC=2
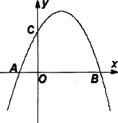
1.求抛物线的解析式及对称轴
2.点E是抛物线在第一象限内的一点,且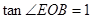 ,求点E的坐标;
,求点E的坐标;
3.在抛物线的对称轴上,是否存在点P,使得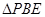 为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2011年重庆名校中考数学函数综合试题精练 题型:选择题
已知,抛物线 与x轴交于
与x轴交于 和
和 两点,与y轴交于
两点,与y轴交于 。
。

1.求这条抛物线的解析式和抛物线顶点M的坐标
2.求四边形ABMC的面积;
3.在对称轴的右侧的抛物线上是否存在点P,使 为直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由
为直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由
查看答案和解析>>
科目: 来源:2011年重庆名校中考数学函数综合试题精练 题型:选择题
如图,直线 分别交
分别交 轴、
轴、 轴于B、A两点,抛物线L:
轴于B、A两点,抛物线L: 的顶点G在
的顶点G在 轴上,且过(0,4)和(4,4)两点.
轴上,且过(0,4)和(4,4)两点.

1.求抛物线L的解析式;
2.抛物线L上是否存在这样的点C,使得四边形ABGC是以BG为底边的梯形,若存在,请求出C点的坐标,若不存在,请说明理由.
3.将抛物线L沿 轴平行移动得抛物线L
轴平行移动得抛物线L ,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L
,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L 上. 试问这样的抛物线L
上. 试问这样的抛物线L 是否存在,若存在,求出L
是否存在,若存在,求出L 对应的函数关系式,若不存在,说明理由.
对应的函数关系式,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com