解方程

某工厂计划招聘A、B两个工种的工人共120人，A、B两个工种的工人月工资分别为800元和1000元．

  (1)若某工厂每月支付的工人工资为ll000O元，求A、B两个工种的工人各招聘多少人?

  (2)若要求B工种的人数不少于A工种人数的2倍，那么招聘A工种的工人多少人时，可使工厂每月支付的工人工资最少?

(1）根据下列步骤画图并标明相应的字母:（直接在图１中画图）

①以已知线段（图1）为直径画半圆；

②在半圆上取不同于点的一点，连接；

③过点画交半圆于点

（2）尺规作图：（保留作图痕迹，不要求写作法、证明）

已知：（图2）．求作：的平分线．

在“3.15”消费者权益日的活动中，对甲、乙两家商场售后服务的满意度进行了抽查. 如图15反映了被抽查用户对两家商场售后服务的满意程度（以下称：用户满意度），分为很不满意、不满意、较满意、很满意四个等级，并依次记为1分、2分、3分、4分.

（1）请问：甲商场的用户满意度分数的众数为     ；乙商场的用户满意度分数的众数为      .

（2）分别求出甲、乙两商场的用户满意度分数的平均值（计算结果精确到0.01）.

（3）请你根据所学的统计知识，判断哪家商场的用户满意度较高,并简要说明理由

暑假期间，小亮到邢台寒山风景区——景区主峰寒山垴（为邢台市太行山段最高峰，位于内邱县境内）旅游，导游提醒大家上山要多带一件衣服，并介绍山区气温会随着海拔高度的增加而下降，沿途小亮利用随身带的登山表（具有测定当前的位置的海拔高度和气温等功能）测得以下的数据：

（1）如图16以海拔高度为x轴，根据上表提供的数据在下列直角坐标系中描点并连线.

（2）观察（1）中所画出的图像，猜想y与x之间函数关系，求出所猜想的函数关系表达式.

（3）如果小亮到达山顶时，只告诉你山顶气温为20.2℃，你能计算寒山垴海拔高度大约是多少米？

在不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.

（1）试求袋中蓝球的个数.

（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率.

如图，给出五个条件：①AE平分∠BAD；②BE平分∠ABC；③E是CD的中点，④AE⊥EB；⑤AB＝AD+BC.

（1）请你以其中三个作为命题的条件，写出一个能推出AD∥BC的正确命题，并加以说明；

（2）请你以其中三个作为命题的条件，写出一个不一定能推出AD∥BC的正确命题，并举例说明

已知AB为⊙O的直径，弦CD⊥AB，垂足为H.求证：AH•AB=AC2

如图19，E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上可以移动的四个点，每组对边上的两个点，可以连接成一条线段.

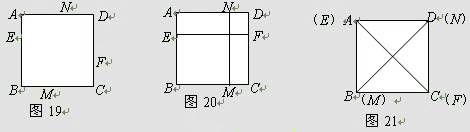
（1）如图20，如果EF∥BC，MN∥CD，那么EF      MN（位置），EF      MN（大小）

（2）如图21，如果E与A，F与C，M与B，N与D重合，那么EF      MN（位置），EF      MN（大小）.

（3）当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时，猜想线段EF、MN满足什么位置关系时，才会有EF＝MN，画出相应的图形，并证明你的猜想.

某污水处理公司为学校建一座三级污水处理池，平面图形为矩形，面积为200平方米（平面图如图所示的ABCD）.已知池的外围墙建造单价为每米400元.中间两条隔墙建造单价每米300元，池底建造的单价为每平方米80元（池墙的厚度不考虑）

（1）如果矩形水池恰好被隔墙分成三个正方形，试计算此项工程的总造价（精确到100元）

（2）如果矩形水池的形状不受（1）中长、宽的限制，问预算45600元总造价，能否完成此项工程？试通过计算说明理由.

（3）请给出此项工程的最低造价（多出部分只要不超过100元就有效）