如图，为了测量河宽AB(假设河的两岸平行)，测得∠ACB＝30°，

∠ADB＝60°，CD＝60m，则河宽AB为        m(结果保留根号)．

18．如图，三个半圆依次相外切，它们的圆心都在x轴上，并与直线y＝x相切．设三个半圆的半

径依次为r₁、r₂、r₃，则当r₁＝1时，r₃＝       ．

(10分)(1)计算：2²＋(－1)⁴＋(－2)⁰－|－3|；

(2)先化简，再求值：(4ab³－8a²b²)÷4ab＋(2a＋b)(2a－b)，其中a＝2，b＝1．

(8分)求不等式组        的解集，并写出它的整数解．

(9分)某中学学生为了解该校学生喜欢球类活动的情况，随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类)，并将调查的结果绘制成如下的两幅不完整的统计图．

请根据图中提供的信息，解答下面的问题：

(1)参加调查的学生共有        人，在扇形图中，表示“其他球类”的扇形的圆心角为        度；

(2)将条形图补充完整；

(3)若该校有2000名学生，则估计喜欢“篮球”的学生共有        人．

(8分)如图，AM切⊙O于点A，BD⊥AM于点D，BD交⊙O

于点C，OC平分∠AOB．求∠B的度数．

(8分)在社区全民健身活动中，父子俩参加跳绳比赛．相同时间内父亲跳180个，儿子跳210个．已知儿子每分钟比父亲多跳20个，父亲、儿子每分钟各跳多少个？

(8分)比较正五边形与正六边形，可以发现它们的相同点和不同点．例如：

它们的一个相同点：正五边形的各边相等，正六边形的各边也相等．

它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形．

请你再写出它们的两个相同点和不同点：

相同点：

①                                               ；

②                                               ．

不同点：

①                                               ；

②                                               ．

(9分)光明中学十分重视中学生的用眼卫生，并定期进行视力检测．某次检测设有A、B两处检测点，甲、乙、丙三名学生各自随机选择其中的一处检测视力．

(1)求甲、乙、丙三名学生在同一处检测视力的概率；

(2)求甲、乙、丙三名学生中至少有两人在B处检测视力的概率．

(10分)如图1，O为正方形ABCD的中心，

分别延长OA、OD到点F、E，使OF＝2OA，

OE＝2OD，连接EF．将△EOF绕点O逆时针

旋转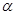角得到△E₁OF₁(如图2)．

(1)探究AE₁与BF₁的数量关系，并给予证明；

(2)当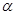＝30°时，求证：△AOE₁为直角三角形．