在3×5的棋盘上，一枚棋子每次可以沿水平或者垂直方向移动一小格，但不可以沿任何斜对角线移动.从某些待定的格子开始，要求棋子经过全部的小正方格恰好一次，但不必回到原来出发的小方格上.在这15个小方格中，有(    )个可以是这枚棋子出发的小方格.

(A)6              (B)8              (C)9            (D)10

正方形ABCD的边长为5，E为边BC上一点，使得BE=3，P是对角线BD上的一点，使得PE+PC的值最小.则PB=        .

设a、b、c为整数，且对一切实数x，(x-a)(x-8)+1=(x-b)(x-c) 恒成立.则a+b+c的值为         .

如图，在以O为圆心的两个同心圆图2中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B.若OM=2，OP= 1，MA=AB=BC，则△MBQ的面积为         .

从1， 2，…， 2 006中，至少要取出        个奇数，才能保证其中必定存在两个数，它们的和为2 008.

(20分)实数x、y、z、w满足x≥y≥z≥w≥0，且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.

(25分)如图，在Rt△ABC中，∠B=90°，它的内切圆分别与边BC、CA、AB相切于点D、E、F，联结AD与内切圆相交于另一点P，联结PC、PE、PF.已知PC⊥PF.求证:

(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.

(25分)在中，有多少个不同的整数(其中，[x]表示不大于x的最大整数)?

如图，抛物线与x轴交A、B两点（A点在B点左侧），直线与抛物线交于A、C两点，其中C点的横坐标为2

1.求A、B 两点的坐标及直线AC的函数表达式；

2.P是线段AC上的一个动点，过P点作y轴的平行线交       

抛物线于E点，求线段PE长度的最大值；

3.点G是抛物线上的动点，在x轴上是否存在点F，

　使A、C、F、G这样的四个点为顶点的四边形是

平行四边形？如果存在，直接写出所有满足条件的F

点坐标；如果不存在，请说明理由

如图，在平面直角坐标系xoy中，矩型ABCD的边AB在x轴上，且AB=3，BC=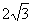，直线y=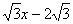经过点C，交y轴于点G

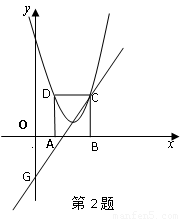
1.点C、D的坐标分别是C（        ），D（        ）

2.求顶点在直线y=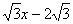上且经过点C、D的抛物线的解析式

3.将（2）中的抛物线沿直线y=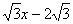平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由。