（本题满分8分）

某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费．某顾客刚好消费200元．

（1）该顾客至少可得到      元购物券，至多可得到    元购物券；

（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．

某校初二全体320名学生在参加电脑培训前后各进行了一次水平相同的考试，考试都以同一标准划分成“不合格、合格、优秀”三个等级，为了了解培训的效果，用抽签的方式得到其中32名学生的两次考试等级，所绘的统计图如图所示，结合图示信息回答下列问题： ⑴这32名学生培训前考分的中位数所在的等级是     ；⑵这32名学生经过培训后，考分等级“不合格”的百分比是   ；⑶估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有  名；⑷你认为上述估计合理吗？理由是什么？

（本题满分8分）

如图，一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出，继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出，求海底黑匣子C点处距离海面的深度？（保留根号）

甲乙两人同时登山，甲、乙两人距地面的高度（米）与登山时间（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：

（1）甲登山的速度是每分钟     米，乙在地提速时距地面的高度为  ____米；

（2）若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度（米）与登山时间（分）之间的函数关系式；

（3）登山多长时间时，乙追上了甲？

如图，AB是⊙O的直径，BC是弦，∠ABC的平分线BD交⊙O于点D，DE⊥BC，交BC的延长线于点E，BD交AC于点F．⑴求证：DE是⊙O的切线；（2） 若CE=1，ED=2，求⊙O的半径．

某公司准备投资开发A、B两种新产品，通过市场调研发现：如果单独投资A种产品，则所获利润（万元）与投资金额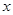（万元）之间满足正比例函数关系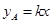：；如果单独投资B种产品，则所获利润（万元）与投资金额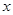（万元）之间满足二次函数关系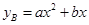：．根据公司信息部的报告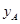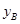，，（万元）与投资金额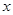（万元）的部分对应值如下表所示：

（1）填空：     ；       ；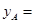

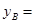（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为w（万元），试写出w与某种产品的投资金额x之间的函数关系式；

（3）请你设计一个在⑵中能获得最大利润的投资方案．

如果一个点能与另外两个点能构成直角三角形，则称这个点为另外两个点的勾股点．例如：矩形ABCD中，点C与A，B两点可构成直角三角形ABC，则称点C为A，B两点的勾股点．同样，点D也是A，B两点的勾股点．

（1）如图1，矩形ABCD中，AB＝2，BC＝1，请在边CD上作出A，B两点的勾股点（点C和点D除外）（要求：尺规作图，保留作图痕迹，不要求写作法）；

（2）矩形ABCD中，AB＝3，BC＝1，直接写出边CD上A， B两点的勾股点的个数；

（3）如图2，矩形ABCD中，AB＝12，BC＝4，DP=4，DM＝8，AN＝5．过点P作直线l平行于BC，点H为M，N两点的勾股点，且点H在直线l上．求PH的长．

如图，菱形ABCD的边长为20cm，∠ABC＝120°．动点P、Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q以2cm/s的速度，沿A→C的路线向点C运动．当P、Q到达终点C时，整个运动随之结束，设运动时间为t秒．

（1）在点P、Q运动过程中，请判断PQ与对角线AC的位置关系，并说明理由；

（2）若点Q关于菱形ABCD的对角线交点O的对称点为M，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N．

①当t为何值时，点P、M、N在一直线上？

②当点P、M、N不在一直线上时，是否存在这样的t，使得△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

若是一元一次方程，则                    （       ）

  (A)1         （B)  2        （C)  -1     （D) -2 .

已知是方程的解，则k的值是                               （　 　）

(A)2　　　   （B)-2　    　 （C)1　      （D) -1